【学习路线图】深度学习从入门到入土

Underwater Acoustic Communication Receiver Using Deep Belief Network
基于深信度网络的水声通信接收机

Abstract

Underwater environments create a challenging channel for communications.
水下环境为通信创造了具有挑战性的信道。
In this paper, we design a novel receiver system by exploring the machine learning technique–Deep Belief Network (DBN)– to combat the signal distortion caused by the Doppler effect and multi-path propagation.
在本文中，我们设计了一种新的接收机系统，通过探索机器学习技术-深度信念网络（DBN）-来对抗由多普勒效应和多径传播引起的信号失真。
We evaluate the performance of the proposed receiver system in both simulation experiments and sea trials. Our proposed receiver system comprises of DBN based de-noising and classification of the received signal.
我们评估所提出的接收机系统在模拟实验和海上试验的性能。我们提出的接收机系统包括基于DBN的去噪和接收信号的分类。
First, the received signal is segmented into frames before the each of these frames is individually pre-processed using a novel pixelization algorithm.
首先，接收到的信号被分割成帧，然后使用新颖的像素化算法对这些帧中的每一个进行单独的预处理。
Then, using the DBN based de-noising algorithm, features are extracted from these frames and used to reconstruct the received signal.
然后，使用基于DBN的去噪算法，从这些帧中提取特征并用于重建接收信号。
Finally, DBN based classification of the reconstructed signal occurs.
最后，发生重构信号的基于DBN的分类。
Our proposed DBN based receiver system does show better performance in channels influenced by the Doppler effect and multi-path propagation with a performance improvement of 13.2dB at 10−3 Bit Error Rate (BER).
我们提出的基于DBN的接收机系统在受多普勒效应和多径传播影响的信道中确实表现出更好的性能，在10−3比特误码率（BER）下性能提高了13.2dB。
Index Terms
索引词
Underwater acoustic communications, receiver systems, machine learning, signal processing, Doppler effect.
水声通信，接收系统，机器学习，信号处理，多普勒效应。

I. INTRODUCTION

Underwater Acoustic Communications (UWAC) is a knowledge rich field that has, in the recent years, gained a tremendous amount of interest for its many applications in the field of ocean exploration, defense, and marine commercial industries.
水下声通信是一个知识丰富的领域，近年来，由于其在海洋勘探、国防和海洋商业领域的许多应用，引起了人们极大的兴趣。
A few notable applications are underwater exploration [1], underwater mine detection [2], and underwater communications between submarines or underwater nodes [3].
一些值得注意的应用是水下勘探[1]，水下地雷探测[2]以及潜艇或水下节点之间的水下通信[3]。
Due to a rapidly growing need for data-heavy underwater systems, the expectations and requirements of the underwater system design has risen up to a point where a growing number of researchers are starting to turn to unconventional methods like machine learning (ML) and deep learning (DL) to combat the challenging underwater environment.
由于对数据密集型水下系统的需求迅速增长，水下系统设计的期望和要求已经上升到一个点，越来越多的研究人员开始转向机器学习（ML）和深度学习（DL）等非传统方法来应对具有挑战性的水下环境。
In this paper, we propose a novel receiver system that utilizes the capabilities of Deep Belief Networks (DBNs) to redesign the de-noising and demodulation blocks of the communication system.
在本文中，我们提出了一种新的接收机系统，利用深度信念网络（DBN）的能力，重新设计的通信系统的去噪和解调块。
Generally, conventional signal processing algorithms in communications are based on strong mathematical foundations and are designed specifically for a variety of specific channels and system models [4], [5].
通常，通信中的传统信号处理算法基于强大的数学基础，并且是专门针对各种特定信道和系统模型而设计的[4]，[5]。
For instance, the Binary Phase-Shift Key (BPSK) modulation was designed for the detection of a constellation symbol in a channel of additive white Guassian noise (AWGN) [6].
例如，二进制相移键控（BPSK）调制被设计用于检测加性白色高斯噪声（AWGN）信道中的星座符号[6]。
These signal processing algorithms are constructed on expert knowledge of the tractable channel models, which in turn are established on a simplification of Maxwell’s equations [7].
这些信号处理算法是基于易处理信道模型的专业知识构建的，而易处理信道模型又是基于麦克斯韦方程的简化而建立的[7]。
UWAC signals, however, are not electromagnetic in nature [8], [9]. As such, the UWAC channel is widely characterized as one of the most complex channels to model and has yet to develop a palpable or definite model.
然而，UWAC信号本质上不是电磁的[8]，[9]。因此，UWAC信道被广泛地表征为最复杂的信道之一，并且尚未开发出明显或明确的模型。
Its high complexity is mostly derived from its fast varying characteristics, such as the Doppler effect and the propagation properties.
其高复杂度主要来源于其快速变化的特性，如多普勒效应和传播特性。
Since communications are heavily reliant on the characteristics of sound, it shows a strong correlation with the properties of sound [8].
由于通信在很大程度上依赖于声音的特性，因此它与声音的属性有很强的相关性[8]。
By understanding how sounds are influenced during sea trials, one can optimize the efficiency of the communication through adaptation.
通过了解在海上试验期间声音是如何受到影响的，人们可以通过适应来优化通信效率。
As sound propagates underwater at a very low speed of approximately 1500 m/s [9], and propagation occurs over multiple paths, it is very common to observe a delay spreading over tens or even hundreds of milliseconds which results in frequency-selective signal distortion.
由于声音在水下以大约1500m/s的非常低的速度传播[9]，并且传播发生在多个路径上，因此观察到延迟扩展超过数十甚至数百毫秒是非常常见的，这导致频率选择性信号失真。
This motion also results in an extreme Doppler effect.
这种运动也会导致极端的多普勒效应。
Multi-path propagation in the ocean is governed by three effects– (1) sound reflecting off underwater surfaces like bubbles and the seabed, (2) sound refraction in the water due to density change, and (3) energy loss [10].
海洋中的多径传播受三种效应控制-（1）声音从水下表面（如气泡和海底）反射，（2）由于密度变化引起的水中声折射，以及（3）能量损失[10]。
These effects will cause an elongation of the path traveled, and thus a time delay.
这些效应将导致行进路径的延长，从而导致时间延迟。
The first also creates reverberation, which causes a reflection phase change and a reflection amplitude change.
第一种也产生混响，这导致反射相位变化和反射幅度变化。
The second is a consequence of the spatial variability of sound speed, which is dependent on temperature, salinity, and pressure.
第二个是声速的空间变化的结果，这取决于温度，盐度和压力。
These factors vary with depth and location.
这些因素因深度和位置而异。
The final effect is heavily dependent on the signal frequency, as well as the pH level of the water.
最终效果在很大程度上取决于信号频率以及水的pH值。
This dependence is a consequence of absorption, where the signal energy is converted to heat.
这种依赖性是吸收的结果，其中信号能量被转换为热量。
In addition to the absorption loss, the signal typically experiences a spreading loss, which increases with distance [8].
除了吸收损耗之外，信号通常会经历扩展损耗，其随着距离的增加而增加[8]。
To correct for the intersymbol interference (ISI) caused by the propagation, the works done in [11]–[13] used an adaptive equalizer to flexibly compensate for the changes in the channel.
为了校正由传播引起的符号间干扰（ISI），[11]-[13]中所做的工作使用自适应均衡器来灵活地补偿信道的变化。
Another distinguishing property of UWAC is the channel’s time variability – (1) inherent changes in the propagation medium and (2) transmitter/receiver motion.
UWAC的另一个显著特性是信道的时间可变性-（1）传播介质的固有变化和（2）发射机/接收机运动。
Inherent changes include long term changes like seasonal temperatures and instantaneous changes caused by shipping routes and moving water surfaces.
内在的变化包括长期的变化，如季节性温度和航运路线和移动水面引起的瞬时变化。
These factors result in both a scattering of the signal and a Doppler effect spreading due to the changing path length [10].
这些因素导致信号的散射和由于路径长度变化而扩展的多普勒效应[10]。
A combination of these factors creates a complex challenge of modeling a sufficiently accurate channel model.
这些因素的组合产生了对足够准确的信道模型进行建模的复杂挑战。
To combat Doppler shifts, many Doppler scale estimation techniques have been proposed as seen in [14], [15].
为了对抗多普勒频移，已经提出了许多多普勒尺度估计技术，如[14]、[15]中所见。
In recent years, ML and more specifically DL have gained recognition for their performance in fields known for their high modelling complexity [16], such as image recognition [17], natural language processing [18], and handwriting analysis [19].
近年来，ML（更具体地说，DL）在以其高建模复杂性而闻名的领域[16]中的表现获得了认可，例如图像识别[17]，自然语言处理[18]和手写分析[19]。
Currently researchers have begun to explore the applications of ML and DL in the area of communications.
目前，研究人员已经开始探索ML和DL在通信领域的应用。
For example, recent research by Wang et al. [20] exploited deep learning to detect signal modulations in underwater channels.
例如，Wang等人最近的研究[20]利用深度学习来检测水下信道中的信号调制。
Other studies like [21], [22] used deep neural network (NN)-based auto encoders to demodulate received signals.
其他研究如[21]，[22]使用基于深度神经网络（NN）的自动编码器来解调接收到的信号。
As such, we can expect that applying ML techniques to communication blocks in order to provide a promising solution to the complex channel problem will yield significant improvements in decoding the physical layer.
因此，我们可以预期，将ML技术应用于通信块以提供对复杂信道问题的有希望的解决方案将在解码物理层方面产生显著的改进。
Works in [23], [24] investigate the use of DL based orthogonal frequency-division multiplexing (OFDM) receiver to recover signals corrupted by the UWAC channel.
在[23]、[24]中的工作研究了使用基于DL的正交频分复用（OFDM）接收机来恢复被UWAC信道破坏的信号。
In this paper, we explore a receiver system that fundamentally rethinks the traditional communications system design.
在本文中，我们探讨了一种接收机系统，从根本上重新思考传统的通信系统设计。
The receiver system utilizes DBNs, more specifically a greedy layer-wise ML algorithm that is able to automatically learn a new latent representation of the data.
接收器系统利用DBN，更具体地说，是一种贪婪逐层ML算法，能够自动学习数据的新潜在表示。
The two main functions of the receiver system are – (1) de-noising the received signal and (2) classifying the signals into their binary representatives.
接收机系统的两个主要功能是：（1）对接收到的信号进行去噪，以及（2）将信号分类成它们的二进制表示。
The features extracted by the DBN are considered as the properties of input data and are formed by considering the output layer of the DBN.
由DBN提取的特征被认为是输入数据的属性，并通过考虑DBN的输出层而形成。
For the first aspect of the proposed receiver, we train a DBN such that it learns to extract features of the received signal.
对于所提出的接收器的第一个方面，我们训练DBN，使得它学习提取接收信号的特征。
The trained DBN distinguishes the features of the segmented pre-processed signal and groups them with the same “clean” framed training data.
训练的DBN区分分段的预处理信号的特征，并将它们与相同的“干净”帧训练数据分组。
Furthermore, DBN is capable of reconstructing the input data based on their reduced, learned representation.
此外，DBN能够基于其简化的学习表示来重建输入数据。
After the DBN, the classification part of our system uses the features which can be tuned by back-propagation for classification.
在DBN之后，我们系统的分类部分使用可以通过反向传播进行分类调整的特征。
The main contributions of this paper are as follows:
本文的主要贡献如下：
1)Developed a de-noising DBN model. The trained DBN model distinguishes the features extracted from a segmented pre-processed signal. It then groups these features with the same “clean” framed training data.
建立了一个去噪DBN模型。训练的DBN模型区分从分段的预处理信号中提取的特征。然后，它将这些特征与相同的“干净”框架训练数据进行分组。
2)Redesigned the demodulation block using a classifying DBN model that utilizes feature extraction and back-propagation for classification of the received signals.
使用分类DBN模型重新设计解调模块，该模型利用特征提取和反向传播对接收信号进行分类。
3)The simulation results show that our proposed DBN based system is able to remain relatively resolute against the different characteristics of the UWAC channel. Furthermore, a sea trial was conducted to verify the performance of the proposed DBN-based receiver system in a real life environment.
仿真结果表明，我们提出的基于DBN的系统是能够保持相对坚决对UWAC信道的不同特性。此外，进行了海上试验，以验证所提出的基于DBN的接收机系统在真实的生活环境中的性能。
The remainder of this paper is organized as follows.
本文的其余部分组织如下。
Section II describes the communication system, underwater channel, and receiver system models.
第二节介绍了通信系统、水下信道和接收机系统模型。
Section III illustrates the proposed DBN based de-noising technique used.
第三节说明了所提出的基于DBN的去噪技术。
Section IV provided a description of the proposed DBN based demodulation technique used in the novel receiver system.
第四节提供了在新颖的接收机系统中使用的所提出的基于DBN的解调技术的描述。
Section V discussed the results of the proposed receiver system and the sea trial used for validation.
第五节讨论了拟议接收器系统的结果和用于验证的海上试验。
Finally, conclusions are drawn in Section VI.
最后，在第六节中得出结论。

II. SYSTEM MODEL OVERVIEW

系统模型概述
In this section, we describe the proposed end-to-end communication system, represented in Fig. 1, comprising of a single transmitter and receiver.
在本节中，我们描述所提出的端到端通信系统，如图1所示，包括单个发射机和接收机。

图一 端到端系统模型
The following subsections will describe the overall communication system model used to test our proposed system, the derivation of the underwater acoustic channel model, and an overview of the proposed receiver system.
以下小节将描述用于测试我们提出的系统的整体通信系统模型、水下声学信道模型的推导以及所提出的接收器系统的概述。

A. Communication System Model
A.通信系统模型
First, let y(n) be the representation of the convoluted transmitted bits, Y(n), and the binary representation of the modulated target transmitted signal z(t) during the n-th transmission.
首先，设y（n）是卷积的发送比特的表示，Y（n），以及在第n次发送期间调制的目标发送信号z（t）的二进制表示。
A series of transmission symbols y(n) are translated into different transmission signal waveforms z(t) via a Phase Shift Key (PSK) modulator as described in [25].
一系列传输符号y（n）通过相移键控（PSK）调制器被转换成不同的传输信号波形z（t），如[25]所述。
Second, let x(t) represent the overall transmitted signal consisting of z(t) and a Hyperbolic Frequency Modulated (HFM) pilot [26]. x(t) is then relayed through a channel model to obtain the received signal s(t):
其次，让x（t）表示由z（t）和双曲调频（HFM）导频组成的总发射信号[26]。x（t）然后通过信道模型被中继以获得接收信号s（t）：

where H(t) is the channel equation, · represents the dot product, and no(t) is the Additive White Gaussian Noise (AWGN).
其中H（t）是信道方程，·表示点积，no（t）是加性白色高斯噪声（AWGN）。
Finally, we generate a set of training data [zt,yt], t = 1, 2,… ,n,where zt is a training signal, yt is the corresponding BPSK binary label vector consisting of 0s and 1s, and n is the number of the training signals.
最后，我们生成一组训练数据[zt，yt]，t = 1，2，.，n，其中zt是训练信号，yt是由0和1组成的对应BPSK二进制标记向量，n是训练信号的数目。
Once detection and removal of the HFM pilot is completed, the desired section of the received signal s (t) acts as the input for the proposed receiver system.
一旦完成HFM导频的检测和去除，接收信号的期望部分(t)用作所提出的接收机系统的输入。
The algorithm will build a model from the training data L, such that for a given s’(t), the trained model will be able to predict a reconstructed waveform ˜z(n) and its corresponding label ˜y(n).
该算法将从训练数据L构建模型，使得对于给定的s'(t)，训练的模型将能够预测重构的波形˜z（n）及其对应的标签˜y（n）。
Therefore, predicting the received bits, ˜Y(n).
因此，预测所接收的比特，˜Y(n)

B. Underwater Channel
B.水下信道
Underwater acoustic communication channels are regarded by researchers as one of the most complex communication channels to model. Multi-path propagation and Doppler effects are recognized as one of the most challenging factors of the underwater acoustic channel [27]–[29].
水声通信信道被认为是最复杂的通信信道之一。多径传播和多普勒效应被认为是水声信道最具挑战性的因素之一[27]-[29]。
The more common techniques to approximately simulate the underwater acoustic channel vary from signal-to-noise ratio (SNR)-based channel models tha channel vary from signal-to-noise ratio (SNR)-based channel models that rely on empirical equations as seen in [8] to models that are based on the assumption of Rayleigh signal fading in [30], [31].
近似模拟水下声学信道的更常见的技术从基于信噪比（SNR）的信道模型到基于瑞利信号衰落的假设的模型，其中信道从依赖于如[8]中所见的经验方程的基于信噪比（SNR）的信道模型变化[30]、[31]。
In this subsection, the channel model used for the simulation will be presented, taking into consideration multi-path propagation and Doppler effect.
在本小节中，将给出用于仿真的信道模型，考虑多径传播和多普勒效应。
1)Multi-Path Propagation: Multi-path propagation in the ocean is mostly governed by sound reflecting off underwater surfaces like bubbles and the seabed [32]. These effects will cause an elongation of the path traveled, and thus a time delay. The received signal in a mutli-path environment can be generally represented as seen in [33], [34]:
多路径传播：海洋中的多径传播主要由气泡和海底等水下表面反射的声音控制[32]。这些效应将导致行进路径的延长，从而导致时间延迟。多径环境中的接收信号通常可以如[33]、[34]中所示表示：

where A represents the reverberation created by the reflection and scattering. This phenomena results in a reflection phase change and a propagation loss [32]. As such, Eq. 2 can be further expressed as:
其中A表示由反射和散射产生的混响。这种现象导致反射相位变化和传播损耗[32]。因此，Eq。2可以进一步表示为：

where a^a_i is the amplitude variation caused by the reverberation and fading of the channel, ◦ represents the Hadamard product, and a^b_i (θ(t)) is the phase variation and is modeled as seen in [35]:
其中a^a_i是由信道的混响和衰落引起的幅度变化，θ i表示Hadamard乘积，并且a^b_i (θ(t))是相位变化，并且如[35]中所示建模：

where j represents the imaginary number, k is the length of the signal and θ_k is the phase shift corresponding to the change in angle.
其中j表示虚数，k是信号的长度，θ_k是对应于角度变化的相移。
2)Doppler Effect: In underwater communications, a combination of the low speed of underwater sound propagation and the relative movement of the transmitter and receiver introduces the Doppler effect [8]. Let v denote the speed of the relative movement of the transmitter and the receiver, and fc denote the carrier frequency of the transmitted signal. The carrier frequency at the receiver is given by:
多普勒效应：在水下通信中，水下声音传播的低速和发射器和接收器的相对运动的组合引入了多普勒效应[8]。设v表示发射器和接收器的相对运动速度，fc表示发射信号的载波频率。接收器处的载波频率由下式给出：

where Δs denotes the sound propagation speed underwater. Note that Δrt is positive in the event that the receiver is moving toward the transmitter, otherwise Δrt is negative.
其中Δs表示水下的声音传播速度。注意，如果接收器正向发射器移动，则Δrt为正，否则Δrt为负。
In the time domain, the Doppler effect can be construed as a lengthening or compression of the transmitted waveform [36], [37]. The Doppler effect can be depicted in the time-domain as:
在时域中，多普勒效应可以被解释为发射波形的延长或压缩[36]，[37]。多普勒效应可以在时域中描述为：

where α is the Doppler co-efficient.
其中α是多普勒系数。
Taking into consideration the above contributing characteristics, the channel model used in this paper is:
考虑到上述贡献特性，本文中使用的信道模型为：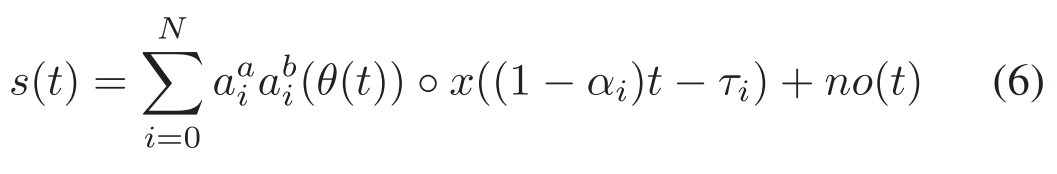

C. Receiver System Model
C.接收机系统模型
The receiver model is comprised of two blocks – (1) de-noising and (2) demodulation.
接收器模型由两个模块组成-（1）去噪和（2）解调。
In the de-noising component, the input signal s’(t) is first converted and normalized into a pixelized matrix m(t) via the proposed pre-processing method. m(t) is then partitioned into i number of m_i(t) to meet the requirement of the proposed algorithm for feature extraction. The learning features of the training data is used to find the closest match to the features of m_i(t), which is then used as a basis for reconstruction via:
在去噪组件中，输入信号s'(t)首先通过所提出的预处理方法将m(t)转换并归一化为像素化矩阵m(t)。然后将m(t)划分为i个m_i(t)，以满足所提出的算法对特征提取的要求。训练数据的学习特征用于找到与m_i(t)的特征最接近的匹配，然后将其用作重建的基础，通过：

where Ψ(·) is a learning function, W and b represents the weights and bias of the network.
其中，Ψ(·)是学习函数，W和b表示网络的权重和偏置。
In the demodulation block, the reconstructed waveform ˜z is classified to a label y˜(n) via:
在解调块中，通过以下方式将重构波形˜z分类为标签y˜(n) ：

where Φ(·) is a learning function.
其中Φ(·)是学习函数。
The focus of this paper is then to optimize the learning functions, Ψ(·) and Φ(·), and their corresponding weights and bias.
然后，本文的重点是优化学习函数，Ψ(·)和 Φ(·)，以及它们相应的权重和偏差。

III. PROPOSED DBN-BASED DE-NOISING

基于DBN的去噪方法
In this section, the de-noising algorithm, consisting of both the pre-processing method and the de-noising DBN, is described. An overview of our proposed algorithm is shown in Fig.2.
在本节中，描述了由预处理方法和去噪DBN组成的去噪算法。我们提出的算法的概述如图2所示。

图二 去噪模块概述
The input is the received signal s (t) and the output is the reconstructed signal ˜z(t).
输入是接收信号s(t)并且输出是重构的信号˜z(t)。

A. Pre-Processing
A.预处理
The pixelization method is defined as:
像素化方法定义为：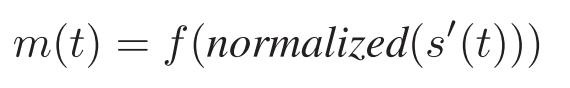

The input signal s’(t) is first normalized into the range of 0 to 1.
输入信号s'(t)首先归一化到0到1的范围内。
We then proceed to pixelize the signal to form m(t).
然后我们继续对信号进行像素化以形成m(t)。


Let Pix be the number of pixels (length wise), which controls the resolution of the pixelization. The implemented pixelization algorithm is shown in Algorithm 1. The input and output of the pixelization is shown in Fig.3a and Fig.3b respectively.
设Pix为像素数（长度方向），它控制像素化的分辨率。所实现的像素化算法如算法1所示。像素化的输入和输出分别如图3a和图3b所示。
Fig. 3. Visualization of the Pre-processing Block Diagram presents the received signal (input) and the pixelized matrix mi(t) (output). The received signal is pre-processed into 4 matrices to provide the DBN based de-noising algorithm with more features to extract.
图三 预处理框图的可视化呈现了接收信号（输入）和像素化矩阵mi(t)（输出）。接收信号被预处理成4个矩阵，以提供基于DBN的去噪算法，以提取更多的特征。
Lastly, m(t) is resized to various resolutions, as shown in Fig. 3. This allows for more features to be extracted and used for the reconstruction.
最后，将m(t)调整为各种分辨率，如图3所示。这允许提取更多的特征并用于重建。

B. De-Noising DBN (Stacked RBMs)
B 去噪DBN（Stacked RBM）
DBNs are probabilistic generative algorithms which provide a joint probability distribution over observable data and labels.
DBN是概率生成算法，其提供可观察数据和标签的联合概率分布。
Restricted Boltzmann Machines (RBMs) are the building blocks of a DBN. Hence, in this section first we briefly describe RBMs and then we will explore DBN.
受限玻尔兹曼机（RBM）是DBN的构建块。因此，在本节中，我们首先简要介绍RBM，然后我们将探讨DBN。

图4 由堆叠RBM组成的DBN的概述。
Fig.4 illustrates the concept of stacking RBMs to form a DBN.
图4示出了堆叠RBM以形成DBN的概念。
A Boltzmann Machine (BM) is a particular form of a Markov Random Field (MRF), where its energy function is linear in its free parameters.
玻尔兹曼机（BM）是马尔可夫随机场（MRF）的一种特殊形式，其能量函数在其自由参数中是线性的。
Some of its variables (hidden units) allow the machine to represent complicated distributions internally. However, they are unobserved.
它的一些变量（隐藏单元）允许机器在内部表示复杂的分布。然而，它们未被观察到。

1. RBMs: The energy function of the joint configuration in Boltzmann machines is given as follows:
   RBM：玻尔兹曼机中关节构型的能量函数如下所示：
   
   where the visible nodes v ∈ R correspond to the input and uv is the number of visible nodes, the hidden nodes h ∈ R represent the latent features and uh is the number of hidden nodes, W represents the concurrent weights linking the nodes of the visible to the hidden layer, b and c are the bias terms of the hidden and visible nodes respectively.
   其中可见节点v ∈ R对应于输入，uv是可见节点的数量，隐藏节点h ∈ R表示潜在特征，uh是隐藏节点的数量，W表示将可见节点链接到隐藏层的并发权重，b和c分别是隐藏节点和可见节点的偏置项。
   The free energy can also be expressed in the following form:
   自由能也可以用以下形式表示：
   
   Because visible and hidden units are conditionally independent of one-another, the following equations hold true.
   因为可见和隐藏单元是有条件地相互独立的，所以下面的等式成立。
   
   When binary units are used, so that vj and hk ∈ 0, 1,and a probabilistic version of the usual neural activation is obtained:
   当使用二进制单位时，使得vj和hk ∈ 0，1，并且获得通常神经激活的概率版本：
   
   The free energy of an RBM with binary units becomes
   具有二进制单位的RBM的自由能变为
   
   Since RBMs are energy based algorithms, i.e. they associate a scalar energy to each configuration of the variables of interest, training them corresponds to modifying that energy function so that its shape has desirable properties, such as low energy configurations.
   由于RBM是基于能量的算法，即它们将标量能量与感兴趣的变量的每个配置相关联，因此训练它们对应于修改该能量函数，使得其形状具有期望的属性，例如低能量配置。
   Energy-based probabilistic models define a probability distribution through an energy function, as follows:
   基于能量的概率模型通过能量函数定义概率分布，如下所示：
   
   where Q is the partition function that is obtained via:
   其中，Q是通过下式获得的配分函数：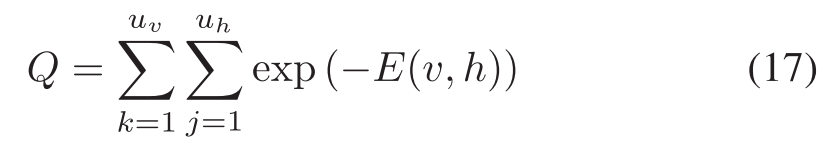
   
   To optimize the parameters of the network at each layer k, the following optimization problem shown by Eqn. 18 is minimize via partial differentiation with respects to W, b, c.
   为了优化每个层k处的网络的参数，下面的由等式11所示的优化问题。18通过关于W、B、c偏微分最小化。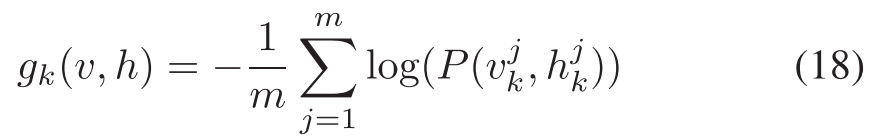
   

2. Stacking RBMs Into a DBN: ADBN is comprised of stacked restricted Boltzmann machines with a fast-learning algorithm that allows the structure to achieve better results with less computational effort.
   将RBM堆叠到DBN中：ADBN由堆叠的受限玻尔兹曼机组成，具有快速学习算法，允许结构以更少的计算工作量获得更好的结果。
   It models the joint distribution between an observed vector x and l hidden layers hk as follows:
   它对观测向量x和l个隐藏层hk之间的联合分布建模如下：
   
   where x = h0, P(hk|hk+1)) is a conditional distribution for the visible units conditioned on the hidden units of the RBM at level k,and P(hl−1|hl) is the visible-hidden joint distribution (output).
   其中x = h 0，P(hk|hk+1)) 是以水平k处的RBM的隐藏单元为条件的可见单元的条件分布，并且P(hl−1|hl)是可见-隐藏联合分布（输出）。

3. Training: To train a DBN such that it can perform matrix de-noising, the normalized pixel values of the pixelized signal are used as input. By using min-max normalization, mi(t) is transformed into a floating-point number system with a range of 0 and 1.
   训练：为了训练DBN，使其可以执行矩阵去噪，将像素化信号的归一化像素值用作输入。通过使用最小-最大归一化，mi(t)被转换成范围为0和1的浮点数系统。
   The main idea is to train a DBN to be able to associate noisy mi(t) to mi(t) with lower noise or no noise.
   主要思想是训练DBN，使其能够将有噪声的mi(t)与具有较低噪声或无噪声的mi(t)相关联。
   This idea can be implemented by learning the features extracted from the noisy and clean mi(t) contents.
   这个想法可以通过学习从噪声和干净的mi(t)内容中提取的特征来实现。
   These features are then presented in some nodes at the last layer of the network.
   然后，这些特征在网络的最后一层的一些节点中呈现。
   The network is trained with a variety of noisy mi(t) as input and clean mi(t) as the desired output.
   该网络是用各种噪声mi(t) 作为输入和干净mi(t) 作为期望输出来训练的。
   Using a standard basis called relative activity to detect noise nodes, each node is defined as the difference between two values of a particular node which results from feeding the network a clean mi(t) and its corresponding noisy mi(t).
   使用称为相对活动的标准基础来检测噪声节点，每个节点被定义为特定节点的两个值之间的差，这是通过向网络馈送干净的mi(t)及其相应的噪声mi(t)而产生的。
   As a result, if a particular node is a noise node, it should have higher relative activity.
   因此，如果特定节点是噪声节点，则它应该具有较高的相对活动性。
   On the other hand, if it is a clean noiseless node, it should have a lower relative activity.
   另一方面，如果它是一个干净的无噪声节点，它应该有一个较低的相对活动。
   This theory is justified by the fact that the activation of mi(t) nodes should be same for both clean noiseless and its corresponding noisy mi(t).
   该理论通过以下事实来证明：对于干净的无噪声和其对应的有噪声mi（t），mi(t)节点的激活应该是相同的。
   By performing the above action for all mi(t) and averaging the values of the last layer’s nodes, the average relative activity of the last layer is computed. The nodes with a higher average relative activity are still viewed as noise nodes.
   通过对所有mi(t)执行上述动作并对最后一层的节点的值求平均，计算最后一层的平均相对活动。具有较高平均相对活性的节点仍然被视为噪声节点。
   Once the noise nodes are discovered, the next step is to lower their activity by selecting the average value of all the noise nodes as their neutral values.
   一旦发现了噪声节点，下一步就是通过选择所有噪声节点的平均值作为它们的中性值来降低它们的活动性。
   As such, the noise nodes are then considered inactive and a clean noiseless mi(t) can be reconstructed.
   因此，噪声节点然后被认为是不活动的，并且可以重建干净的无噪声mi(t)。

C. Results of DBN Based De-Noising
C.基于DBN的去噪结果
In this subsection, we evaluate the proposed DBN based de-noising technique.
在本小节中，我们评估了所提出的基于DBN的去噪技术。
As a baseline for comparison, we used the conventional MLE method devised in [38] and the de-noising auto encoder in [39].
作为比较的基线，我们使用[38]中设计的传统MLE方法和[39]中的去噪自动编码器。
To analyze the only performance of the de-noising capability, the system used was uncoded.
为了分析去噪能力的唯一性能，所使用的系统未编码。
For the following simulation experiments, the simulated BPSK dataset contains 100,000 transmitted signals periods, in which 50% is used for training, 20% on validation and the remaining 30% on testing.
对于下面的仿真实验，仿真的BPSK数据集包含100，000个发送信号周期，其中50%用于训练，20%用于验证，剩余的30%用于测试。

表二 模拟通道参数随机分布的平均值和标准差
The dataset was generated using Eq.6 and Table.II.
使用等式6和表II生成数据集。
The fc, sampling frequency fs and bit rate Rb of the BPSK signals were set at 2kHz, 40kHz and 1kbits/s.
BPSK信号的fc、采样频率fs和比特率Rb分别设置为2kHz、40 kHz和1 kbits/s。
The frequency of random change, fδ, was 2kHz. For consistency, the de-noising auto encoder used as a comparison in this section was trained using the same dataset.
随机变化频率fδ为2kHz。为了保持一致性，本节中用作比较的去噪自动编码器使用相同的数据集进行训练。
First, we conducted a simulation experiment to evaluate the proposed DBN based de-noising technique’s ability to remove noise for channels with extremely high noise.
首先，我们进行了一个模拟实验，以评估所提出的DBN为基础的去噪技术的能力，以消除噪声信道具有极高的噪声。

图五 AWGN信道下与未编码BPSK的去噪误码率精度比较。为了保持一致性，MLE被用作所有3种方法的解调技术。
Fig.5 shows the Bit Error Rate (BER) of the proposed DBN based de-noising technique under the AWGN channel.
图5示出了所提出的基于DBN的去噪技术在AWGN信道下的误码率（BER）。
As a baseline for comparison, we have provided the BER of the MLE and de-noising auto encoder to highlight the substantial gains for highly negative Eb/No.
作为比较的基线，我们提供了MLE和去噪自动编码器的BER，以突出高度负Eb/No.
A reason for this could be the existence of noise invariable properties in the features extracted by the DBN in the proposed DBN based de-noising technique.
其原因可能是在所提出的基于DBN的去噪技术中由DBN提取的特征中存在噪声不变性质。
Evidence of this can be seen by the converging performance of the algorithm to the baseline as the noise level decreases, resulting in a decrease in functionality of the noise invariant property.
这一点的证据可以通过随着噪声水平降低算法收敛到基线的性能来看出，从而导致噪声不变属性的功能降低。
At BER of 10^−2, the performance of the proposed DBN based de-noising technique has a significantly smaller gain of 2.4dB for de-noising auto encoder and 2.6dB for the MLE.
在BER为10−2时，所提出的基于DBN的去噪技术的性能对于去噪自动编码器具有2.4dB的显著较小的增益，对于MLE具有2.6dB的增益。

图6 在AWGN信道下，所提出的基于DBN的去噪算法的可视化呈现了接收信号（输入）和重构信号（输出）。由洋红线描绘的重构信号相对于由绿色描绘的传输信号（理想输出）示出。
Fig.6 shows a visualization of the de-noising outcome.
图6示出了去噪结果的可视化。
At Eb/No = −30dB, the received signal is highly distorted by the channel noise. However, the proposed technique is still able to partially predict the waveform shape.
在Eb/No = −30dB时，接收信号因信道噪声而严重失真。然而，所提出的技术仍然能够部分地预测波形形状。
At Eb No = −5dB, the waveform can be almost perfectly reconstructed.
在Eb/No = −5dB时，波形几乎可以完美地重建。
The second simulation experiment we conducted tested the algorithm’s ability to remain resolute against multi-path propagation.
第二个仿真实验，我们进行了测试的算法的能力，以保持坚决反对多径传播。
The simulated channel distorted received signals, utilized as test cases in this experiment, were modelled by Eq. 2.
本实验中用作测试案例的模拟信道失真接收信号由公式 2 建模。
The number of multi-paths in the dataset was distributed as 40% 1-path, 30% 2-paths and 30% 3-paths.
数据集中的多路径数量分布为40%的1路径，30%的2路径和30%的3路径。

图7 在多径信道下与未编码BPSK的去噪BER精度比较，在等式3中建模。为了保持一致性，MLE被用作所有3种方法的解调技术。
The results of the experiment are shown in Fig.7.
实验结果如图7所示。
With the increasing number of paths, the BER of the proposed DBN based de-noising algorithm achieves considerable gains while remaining relatively stable in comparison to the de-noising auto encoder and MLE.
随着路径数量的增加，所提出的基于DBN的去噪算法的BER实现了相当大的增益，同时与去噪自动编码器和MLE相比保持相对稳定。
Finally, to test the influence of the Doppler effect on the proposed DBN based de-noising algorithm, a simulation experiment was conducted using Eq.5 for the channel.
最后，为了测试多普勒效应对所提出的基于DBN的去噪算法的影响，使用等式5对信道进行仿真实验。

图8 去噪解调BER精度与未编码BPSK的比较，如公式5所示。为了保持一致性，MLE被用作所有3种方法的解调技术。
Fig.8 depicts the results under three different scenarios, where the α =0.5, 1, 1.5 resulting in a fc =1kHz, 2kHz, 3kHz.
图8描述了三种不同情况下的结果，其中α =0.5，1，1.5导致fc =1kHz，2kHz，3kHz。
The BER of the proposed algorithm for all three scenarios are observed to be similar.
所提出的算法的BER为所有三种情况下观察到的是相似的。
Thus implying that for a certain range of α, the algorithm is able to remain relatively rigid to the influences of the Doppler effect.
因此，这意味着对于α的一定范围，该算法能够对多普勒效应的影响保持相对刚性。

A. Classification DBN
A.DBN分类
For the classification DBN, the same general stacked energy based RBM algorithm is used as described in Section IIIB. The input is the reconstructed signal ˜z(t) and the output consists of the respective binary labels ˜y(n) of 0s and 1s.
对于分类DBN，使用与第IIIB节中所述相同的基于一般堆叠能量的RBM算法。输入是重构信号˜z(t)，输出由0和1的相应二进制标记˜y(n)组成。

B. Determining the Structure of Classification DBN
B.DBN分类结构的确定
To determine the classification DBN structure, we investigated the influence of different network structures on the performance of the algorithm in the classification task at Eb/No = 0dB.
为了确定分类DBN结构，我们研究了不同网络结构对算法在Eb/No = 0dB的分类任务中的性能的影响。

表III 训练时期和节点数对DBN分类的影响
As shown in Table III, we attempted nine different network structures, which consist of a varying number of hidden units, and trained them for a varying number of epochs.
如表III所示，我们尝试了九种不同的网络结构，这些结构由不同数量的隐藏单元组成，并对它们进行了不同数量的训练。
The best classification BER results obtained was using the [1250, 50] structure.
得到的最佳分类BER结果是使用[1250，50]结构。
Although the structure [1250, 100] seems to achieve approximately the same results, the time needed for training is significantly larger.
虽然结构[1250，100]似乎达到了大致相同的结果，但训练所需的时间明显更长。

表IV 在我们提出的分类DBN中使用的最终超参数，DBN由2层RDMS组成
To minimize complexity and maximize the performance of the algorithm, we have chosen to use the structure as illustrated in Table IV.
为了最小化算法的复杂性并最大化算法的性能，我们选择使用如表IV所示的结构。

C. Results of Classification DBN
C.DBN分类结果
In this subsection, we evaluate the proposed classification DBN.
在本小节中，我们评估了所提出的分类DBN。
As a baseline for comparison, we used the conventional MLE method devised in [38] to illustrate the similar performance of the demodulation techniques.
作为比较的基线，我们使用[38]中设计的传统MLE方法来说明解调技术的类似性能。
For the following simulation experiments, the simulated dataset contains 100,000 transmitted signals periods, in which 50% is used for training, 20% for validation, and the remaining 30% for testing.
对于以下仿真实验，仿真数据集包含100，000个发送信号周期，其中50%用于训练，20%用于验证，剩余30%用于测试。
The dataset was generated using a AWGN channel model at a range of Eb/No = −10dB to 30dB. For a fair comparison with MLE, the fc of the BPSK signals is set at 2kHz.
该数据集使用AWGN信道模型在Eb/No = −10dB至30dB范围内生成。为了与MLE进行公平比较，BPSK信号的fc被设置为2kHz。
Using the MLE as a baseline, this experiment illustrates that the demodulation performance level of the proposed classification DBN is similar to MLE.
使用MLE作为基线，该实验说明了所提出的分类DBN的解调性能水平与MLE相似。
The results are shown in Fig. 9. This implies that the classification DBN has learned to extract significant features from the PSK modulation scheme.
结果如图9所示。这意味着分类DBN已经学会从PSK调制方案中提取重要特征。
For a truly fair comparison, the proposed algorithm is also compared to Quadrature Phase Shift Keying (QPSK), derived in [25], without much extra training.
为了进行真正公平的比较，还将所提出的算法与在[25]中导出的正交相移键控（QPSK）进行比较，而无需进行过多的额外训练。
As seen, at BER 10−3, the algorithm’s performance for QPSK has a BER of 0.67dB less in comparison to MLE.
如图所示，在BER 10−3时，该算法对QPSK的性能比MLE低0.67dB。
A more inclusive training dataset for higher-order modulation schemes could increase the performance of the algorithm in this area.
高阶调制方案的更具包容性的训练数据集可以提高该算法在这一领域的性能。

V. RESULTS AND DISCUSSION

结果和讨论
This section will evaluate the proposed receiver as a whole as seen in Fig.1.
本节将评估所提出的接收器作为一个整体，如图1所示。
First, the performance of the receiver will analyzed using the simulated underwater model shown in Eq.6.
首先，将使用等式6中所示的模拟水下模型来分析接收器的性能。
Then, the conditions of the conducted sea trial will be described.
然后，将描述所进行的海上试验的条件。
Finally, the collected sea trial data was used to validate the real application of the proposed receiver system.
最后，利用采集的海试数据验证了接收机系统的真实的应用。

图10 传输数据结构。
The data frame of the testing dataset used in both the simulation experiments and sea trials is shown in Fig.10.
在模拟实验和海上试验中使用的测试数据集的数据框架如图10所示。
The pilot consists of a single up-sweep and a down-sweep HFM signal, which is used for detection of the incoming received data signal.
导频由单个上扫和下扫HFM信号组成，其用于检测输入的接收数据信号。
The HFM modulated signal has a bit rate of 50 bits/s and a frequency range of 1-4kHz.
HFM调制信号具有50比特/秒的比特率和1-4kHz的频率范围。
The data frame includes 416 bits of coded BPSK modulated signals.
数据帧包括416比特的编码BPSK调制信号。

表V 模拟和海上试验数据集的规格
The specifications of the data structure is recorded in Table.V.
数据结构的规范记录在表V中。

A. Simulation Overall Results
A.模拟总体结果
In this subsection, we evaluate the overall proposed receiver system.
在这一小节中，我们评估了整个拟议的接收机系统。
To assess performance under a underwater environment, we will be employing 5 systems for evaluation – (1) MLE demodulation, (2) de-noising auto encoder with MLE demodulation, (3) the proposed DBN based receiver, (4) DL orthogonal frequency-division multiplexing (OFDM) [23], and (5) SIC DL [24].
为了评估水下环境下的性能，我们将采用5种系统进行评估-（1）MLE解调，（2）具有MLE解调的去噪自动编码器，（3）提出的基于DBN的接收器，（4）DL正交频分复用（OFDM）[23]，以及（5）SIC DL [24]。
For the following simulation experiments, the training data and channel model used to train the individual parts of the proposed receiver system were the same as stated in Section IV and V.
对于下面的仿真实验，用于训练所提出的接收机系统的各个部分的训练数据和信道模型与第IV和V节中所述的相同。
For equitable contrast, the de-noising auto encoder did not go through any extra training.
为了公平的对比度，去噪自动编码器没有经过任何额外的训练。
The simulated BPSK testing dataset contains 10,000 transmitted signals periods
模拟的BPSK测试数据集包含10，000个发送信号周期

表6 模拟总体通道参数随机分布的平均值和标准差
The dataset was generated using Eq.6 and the random distributions seen in Table.VI.
使用公式6和表VI中的随机分布生成数据集。
The number of multi-paths in the dataset was distributed as 40% 1-path, 30% 2-paths and 30% 3-paths.
数据集中的多路径数量分布为40%的1路径，30%的2路径和30%的3路径。
The dataset contains dataset of 60% 1kHz fδ and 40% 2kHz fδ in each multi-path cluster.
该数据集在每个多径簇中包含60%1kHz fδ和40%2kHz fδ的数据集。
The increase in fδ is used to further simulate the complex occurrence of the underwater scattering.
fδ的增加用于进一步模拟水下散射的复杂发生。
To fairly evaluate the performance of the proposed receiver with the two systems mentioned above, the fc of the BPSK signals is set at 2kHz.
为了公平地评估所提出的接收机与上述两种系统的性能，BPSK信号的fc被设置为2kHz。
In a previous investigation seen in [40], we discovered that the feature extraction ability of the DBN has created a characteristic that is invariant to the influences of the Doppler effect.
在[40]中看到的以前的研究中，我们发现DBN的特征提取能力已经创建了一个对多普勒效应的影响不变的特征。
Therefore, we assume that even though the classification DBN was only trained on fc =2kHz, the performance of the proposed classification DBN will not be significantly degraded by the range of fc used in the testing dataset used.
因此，我们假设即使分类DBN仅在fc =2kHz上训练，所提出的分类DBN的性能也不会因所使用的测试数据集中使用的fc范围而显著降低。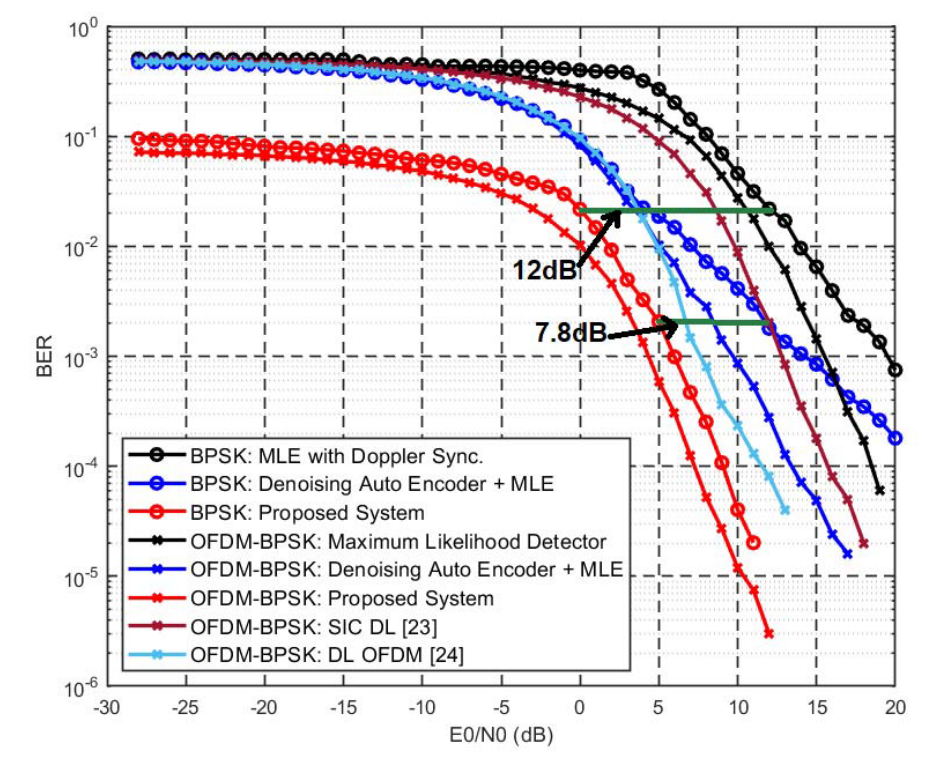

图11 在模拟水下条件下，与编码BPSK和OFDM-BPSK的BER精度比较，由等式6建模。
Fig.11 depicts the performance of the five systems with regards to the above described testing scenario.
图11描绘了关于上述测试场景的五个系统的性能。
The proposed receiver (consisting of both DBN De-noise and DBN Classification) is seen to outperform the other algorithms over a large range of Eb No for both uncoded BPSK and OFDM-BPSK.
所提出的接收机（包括DBN去噪和DBN分类）被认为是优于其他算法在大范围的Eb No的未编码的BPSK和OFDM-BPSK。
This implies that the proposed receiver system is able to remain invariant to changes in instantaneous amplitude, phase and frequencies, such that the shown coding gain can be achieved.
这意味着所提出的接收机系统能够对瞬时幅度、相位和频率的变化保持不变，使得可以实现所示的编码增益。

表VII 算法推理复杂性比较
Table.VII compares the computational complexity of the five algorithms, where n represents input size n for each function.
表VII比较了五种算法的计算复杂度，其中n表示每个函数的输入大小n。
The results show that our proposed system requires a large amount of training time in comparison to the auto encoder and MLE.
结果表明，我们提出的系统需要大量的训练时间相比，自动编码器和MLE。
However, shown in Fig.11, our proposed algorithm outperformed the auto encoder and MLE by 7.8dB and 12dB at Eb/N0 =5 and Eb/N0 =0 respectively for the BPSK modulated system.
然而，如图11所示，对于BPSK调制系统，我们提出的算法在Eb/N0 =5和Eb/N0 =0时分别优于自动编码器和MLE 7.8dB和12dB。

B. Sea Trial Set-up
B.海上试航设置

图12a 海试端到端系统图
The communication system used in the underwater acoustic sea trial is depicted in Fig.12a.
图12a描述了水声海上试验中使用的通信系统。
Before transmission, the desired transmitted signal x(t) is converted from digital values to analog sensor signals using a National Instruments-Data Acquisition (NI-DAQ) hardware unit. The signal is then amplified before being transmitted.
在传输之前，使用National Instruments-Data Acquisition（NI-DAQ）硬件单元将期望的传输信号x(t)从数字值转换为模拟传感器信号。然后，信号在传输之前被放大。
At the receiver end, the signal is first received by the hydrophone and amplified by ISO-TECH IPS-3303.
在接收器端，信号首先由水听器接收并由ISO-TECH IPS-3303放大。
The corresponding NI-DAQ will translate the analog sensor signal to digital values for the proposed communication system.
相应的NI-DAQ将模拟传感器信号转换为数字值，用于拟议的通信系统。
In March 2019, a sea trial was conducted in the waters near Selat Pauh, Singapore, where the bottom is muddy with the deepest depth of approximately 25m.
2019年3月，在新加坡宝海峡附近的沃茨进行了海试，该水域底部泥泞，最深处约25米。
The waters is considered to be relatively stationary with occasional disturbance from the large vessels traveling to the port.
该沃茨被认为是相对静止的，偶尔会有大型船只驶入港口。
In this trial, the distance and depth of the transmitter and receiver was kept at about 300m and 9m respectively, with a variation of 50m and 1m due to the changing currents.
在这次试验中，发射器和接收器的距离和深度分别保持在300米和9米左右，由于水流的变化，变化了50米和1米。
The carrier frequency of the BPSK modulated signal was varied at 1kHz intervals for different trials.
对于不同的试验，BPSK调制信号的载波频率以1kHz的间隔变化。
The trials were conducted at fc =1kHz, fc =2kHz, fc =3kHz and fc =4kHz.
试验在fc =1kHz、fc =2kHz、fc =3kHz和fc =4kHz下进行。
Due to the limitations of the hardware used in the trial, the sampling rate was set at 40 kHz.
由于试验中使用的硬件的限制，采样率设置为40 kHz。

表八 试航规格
The specifications of the sea trial is recorded in Table.VIII.
海试的技术要求见表VIII。

C. Sea Trial Results
C.海上试验结果
In this subsection, the collected data from the sea trial described in Section V-B was used to validate the real application of the proposed receiver system.
在本小节中，使用第V-B节中描述的海上试验中收集的数据来验证拟议接收器系统的真实的应用。

表九 带多普勒同步的MLE和建议的接收器系统之间的SEA试验数据结果和精度比较
The results of which are shown in Table.IX.
其结果见表九。
The estimated average α was calculated using the up and down sweep of the HFM pilot signal and the SNR was estimated using MATLAB.
使用HFM导频信号的上下扫描计算估计的平均α，并且使用MATLAB估计SNR。
For this evaluation, we collected data for 10 trials.
在本次评估中，我们收集了10项试验的数据。
Trial 1-4 were conducted on Day 1 and the results obtained from the sea trial were significantly better than seen in Fig.11 with the most significant on Exp.3 with an coded BER of 0.0093 in comparison to BER of 0.045.
试验1-4在第1天进行，从海上试验中获得的结果明显好于图11中所示，其中实验3最显著，编码BER为0.0093，而BER为0.045。
This implies that during Day 1, the complexity of the channel was significantly lower than that simulated in the above trial.
这意味着在第1天期间，通道的复杂性显著低于上述试验中模拟的复杂性。
The data collected from Trials 5 and 6 on Day 2 had a much lower performance significance with an improvement of 0.08.
在第2天从试验5和6收集的数据具有低得多的性能显著性，改善为0.08。
On Day 3, while carrying out Exp. 7-10, we experienced heavy rain, which resulted in a more complex dataset.
在第3天，当执行Exp.7-10，我们经历了大雨，这导致了一个更复杂的数据集。
As such, the BER seen from the sea trials conducted on Day 3 shows similar performance to the simulated results.
因此，从第3天进行的海上试验中看到的BER显示出与模拟结果相似的性能。
Overall, our proposed receiver system is able to keep a significant performance improvement from the 10^−1 BER of the MLE with Doppler sync. to a 10^−2 BER.
总的来说，我们提出的接收机系统能够保持显着的性能改善，从10^-1误码率的MLE与多普勒同步。10^-2 BER

VI. CONCLUSION AND OUTLOOK

结论与展望
In this paper, we have proposed a novel receiver system that uses DBNs to redesign the de-noising and demodulation techniques for underwater acoustic communications.
在本文中，我们提出了一种新的接收机系统，使用DBNs重新设计的去噪和解调技术的水声通信。
Our approach has also provided an interesting and important pathway for the application of machine learning techniques to underwater communications systems.
我们的方法也为机器学习技术在水下通信系统中的应用提供了一条有趣而重要的途径。
Firstly, although the performance of the receiver system matches performance of traditional systems, without significant improvement, in the AWGN channels, it does show better performance in the more realistically simulated underwater channels influenced by Doppler and multi-path.
首先，虽然该接收机系统的性能与传统系统的性能相匹配，但在AWGN信道中没有显着改善，但在更真实地模拟的受多普勒和多径影响的水下信道中，它确实表现出更好的性能。
A comparison with the traditional MLE and the promising de-noising auto encoder was completed in various underwater scenarios.
与传统的MLE和有前途的去噪自动编码器在各种水下场景的比较完成。
These simulated experiments revealed extremely competitive BER performances with a performance improvement of 13.2dB at 10^−3 BER.
这些模拟实验显示了极具竞争力的BER性能，在10^−3 BER时性能提高了13.2dB。
Therefore, demonstrating the powerful potential for machine learning to be used in more complex underwater acoustic channels.
因此，展示了机器学习在更复杂的水声信道中的强大潜力。
As a further investigation, we will increase the complexity by accommodating different mixtures of noise like rayleigh noise and exponential noise.
作为进一步的研究，我们将增加复杂性，通过容纳不同的混合噪声，如瑞利噪声和指数噪声。
As an additional step, we collected real life data, through a sea trial, to analyze the performance of the proposed receiver in a real scenario.
作为附加步骤，我们通过海上试验收集了真实的寿命数据，以分析所提出的接收器在真实的场景中的性能。
The results of which were promising with a substantial improvement from a coded 10^−1 BER using the traditional MLE method with Doppler synchronization to a coded 10^−2 BER with the proposed receiver.
其结果是有希望的，从使用具有多普勒同步的传统MLE方法的编码10^-1 BER到使用所提出的接收器的编码10^-2 BER有了实质性的改善。
This implies the real possibility of designing machine learning based underwater acoustic communication systems.
这意味着设计基于机器学习的水声通信系统的真实的可能性。
Finally, the strength of using DBNs to design our proposed receiver is denoted by its seemingly learned ability to comprehend and classify differing sets of received signals.
最后，使用DBN来设计我们提出的接收器的强度由其看似学习的能力来理解和分类不同的接收信号集来表示。
Despite the varying parameters– frequency, amplitude, phase and time frames between each random shift– of the scenarios we have chosen to examine the receivers under, our proposed receiver has remained relatively invariant with the largest variation of 5.2dB at an uncoded 10^−4 BER between the presence of 1-path and 3-paths.
尽管我们选择在不同的场景下检查接收器的参数-频率，幅度，相位和每个随机偏移之间的时间帧-，我们提出的接收器保持相对不变，在1-路径和3-路径之间的未编码10^-4 BER下的最大变化为5.2dB。
This phenomena suggests that the DBNs have successfully extracted meaningful features from the signals that could potentially be unchanged to the fluctuations of the underwater channel.
这种现象表明，DBN已经成功地从信号中提取了有意义的特征，这些特征可能对水下信道的波动保持不变。

笔记

摘要

本文介绍了一种新的水下通信接收机系统，采用深度信念网络（DBN）技术应对多普勒效应和多径传播引起的信号失真。使用新的像素化算法将信号切分成帧，然后用基于DBN的去噪算法提取特征重建接收信号，最后对重构信号进行分类。
实验结果显示，该系统在受多普勒效应和多径传播影响的信道中性能优越，10−3比特误码率（BER）下性能提高了13.2dB。

引言

水声通信在海洋等领域具有许多应用，数据密集型水下系统需求增长。但水下环境为通信带来挑战，主要有两个方面：
(1)声波在水下传播速度很低，并在多个路径上传播，因此存在延迟，导致信号失真。
(2)声在水下表面反射、密度变化引起折射、能量损失引起时间延时。

研究学者已经探索机器学习和深度学习在通信领域的应用。例如，Y. Wang, “Modulation classification of underwater communication with deep learning network,” 利用深度学习来检测水下信道中的信号调制。其他研究如V. Q. Dang and Y. Pei, “A study on feature extraction of handwriting data using kernel method-based autoencoder,”使用基于深度神经网络的自编码器来调解接收信号。因此，我们可以预期，将ML技术和DL应用于通信块，将在物理层解码方面产生显著的改进。