【学习路线图】深度学习从入门到入土

基于信道状态信息的水声传感器网络测距

Abstract

Received signal strength (RSS)-based ranging is a promising distance estimation approach in underwater acoustic sensor networks (UASNs). However, the multipath-rich underwater environment complicates acoustic propagations and derails the RSS-based ranging. To address the challenges, this article provides a novel ranging method, called channel state information (CSI)-based ranging for UASNs (CRUN). Instead of RSS, the measured CSI is modeled as a set of power-loss-based equations. Then, the ranging process under multipath scenarios is transformed as a multivariate optimization problem which involves parameters of all propagation paths. This optimization problem aims to simultaneously realize distance estimation and multipath mitigation. Noticing the large number of variables makes the solution numerically unstable, a threshold-windowbased algorithm is proposed to simplify the multivariate optimization problem. In specific, the proposed algorithm extracts relative amplitude attenuations and relative time delays between the line-of-sight (LOS) path and each of the non-line-of-sight paths from CSI. The extracted parameters, being as equality constraints, simplify the multivariate optimization problem to a univariate optimization problem only concerning the desired LOS distance. Then, the simplified problem can be efficiently solved by the gradient descent algorithm. Statistical-channel-model-based simulations and lake experiments demonstrate that CRUN significantly improves the ranging accuracy and robustness compared with RSS-based approaches.
在水声传感器网络 （UASNs）中，基于接收信号强度（RSS）的测距是一种很有前途的距离估计方法。然而，多径丰富的水下环境复杂的声传播和脱轨的RSS测距。为了应对这些挑战，本文提出了一种新的测距方法，称为基于信道状态信息（CSI）的水声传感器网络（UASN）测距（CRUN）。代替RSS，测量的CSI被建模为一组基于功率损耗的方程。然后，多径场景下的测距过程转化为一个多变量的优化问题，其中涉及的所有传播路径的参数。该优化问题旨在同时实现距离估计和多径抑制。由于变量数目多会导致解的数值不稳定，提出了一种基于阈值窗口的算法来简化多变量优化问题。具体地说，该算法从CSI中提取视线（LOS）路径和每个非视线路径之间的相对幅度衰减和相对时间延迟。所提取的参数作为等式约束，将多变量优化问题简化为仅涉及期望视距的单变量优化问题。然后，简化的问题可以有效地解决梯度下降算法。基于统计信道模型的仿真和湖上实验表明，与基于RSS的方法相比，CRUN显著提高了测距精度和鲁棒性。
Index Terms—CSI, ranging, RSS, UASN.
索引词——CSI，测距，RSS，UASN。

摘要部分介绍了在水下声学传感器网络（UASNs）中，基于通道状态信息（CSI）的测距方法。目前，接收信号强度（RSS）是在UASNs中常用的测距方法，但在多径环境下存在一些挑战。

为了解决这些挑战，本文提出了一种名为基于信道状态信息的水声传感器网络测距(CRUN)的新型测距方法，使用CSI作为距离估计的指示器。该方法将测得的CSI建模为一组基于功率损耗的方程，并将多路径场景下的测距过程转化为涉及所有传播路径参数的多元优化问题。文中提出了一种基于阈值窗口算法的方法来简化多元优化问题。该算法从CSI中提取相对幅度衰减和相对时间延迟参数，将其作为等式约束，将多元优化问题简化为仅涉及所需LOS距离的单变量优化问题。该简化后的问题可以通过梯度下降算法高效求解。

通过统计-通道模型为基础的仿真和湖泊实验，证明了CRUN相对于基于RSS的方法在测距精度和鲁棒性方面的显著改进。最后，文中提出了关键词，并对未来研究方向进行了讨论。

I. INTRODUCTION

UNDERWATER wireless sensor networks (UWSNs) have attracted massive attention from academic and industrial researchers in exploring oceans and underwater environments in the latest decade [1]. Communication technologies in UWSNs can be divided into three major categories: optical communication, magnetic induction communication, and acoustic communication [2]. The optical communication provides the highest data rate and the lowest link delay among these three technologies. Nevertheless, the optical signal suffers from severe absorption and scattering introduced by underwater channels, resulting in serious inter symbol interference (ISI) and short transmission distance [3]. The magnetic induction communication is a promising alternative because of its inherent advantages in predictable channel responses, negligible propagation delay, and competitive energy consumption. However, its application is limited to a short range by the near acoustic communication [2]. The optical communication provides the highest data rate and the lowest link delay among these three technologies. Nevertheless, the optical signal suffers from severe absorption and scattering introduced by underwater channels, resulting in serious inter symbol interference (ISI) and short transmission distance [3]. The magnetic induction communication is a promising alternative because of its inherent advantages in predictable channel responses, negligible propagation delay, and competitive energy consumption. However, its application is limited to a short range by the near-field property due to the non-propagation of the magnetic wave [2]. The acoustic communication has been attractive for its less attenuation, which makes it capable of providing a long link range up to tens of kilometers, although it also has intrinsic limitations of high transmission delay and low data rate [4]. For the reasons mentioned above, acoustic technology is considered as a preferable choice for underwater wireless communication beyond tens of meters. Based on the acoustic communication, underwater acoustic sensor networks (UASNs) make applications such as environmental monitoring [5], resource exploration [6], and disaster preparation [7] both practical and effective. The performance of the applications mentioned above depends greatly on the accuracy of localization, which is one of the fundamental tasks of UASNs [8]. In general, underwater localization schemes map physical measurements derived from acoustic signals into the relative distance to the reference points, which is referred to as the ranging process [9]. This article focuses on the ranging method for UASNs.
水下无线传感器网络（Underwater wireless sensor networks，UWSNs）在近十年来引起了学术界和工业界研究人员在探索海洋和水下环境方面的大量关注[1]。UWSNs中的通信技术可以分为三大类：光通信，磁感应通信和声学通信[2]。在这三种技术中，光通信提供了最高的数据速率和最低的链路延迟。然而，光信号会受到水下信道的严重吸收和散射，导致严重的符号间干扰（ISI）和短的传输距离[3]。磁感应通信是一种很有前途的替代方案，因为它在可预测的信道响应，可忽略的传播延迟，和竞争力的能量消耗的固有优势。然而，它的应用被近距离声通信限制在短距离内[2]。在这三种技术中，光通信提供了最高的数据速率和最低的链路延迟。然而，光信号会受到水下信道的严重吸收和散射，导致严重的符号间干扰（ISI）和短的传输距离[3]。磁感应通信是一种很有前途的替代方案，因为它在可预测的信道响应，可忽略的传播延迟，和竞争力的能量消耗的固有优势。然而，由于磁波的非传播，其应用被近场特性限制在短范围内[2]。声学通信因其较少的衰减而具有吸引力，这使得它能够提供长达数十公里的长链路范围，尽管它也具有高传输延迟和低数据速率的固有限制[4]。基于上述原因，水声技术被认为是水下无线通信的首选。水声传感器网络（Underwater Acoustic Sensor Networks，UASNs）以水声通信为基础，使环境监测[5]、资源勘探[6]、防灾减灾[7]等应用变得实用而有效。上述应用的性能在很大程度上取决于定位的准确性，这是UASN的基本任务之一[8]。通常，水下定位方案将从声信号导出的物理测量映射到到参考点的相对距离，这被称为测距过程[9]。本文重点研究了无人自定位系统的测距方法。
In UASNs, physical measurements in the ranging process can be collected by one of the following methods: time of arrival (TOA), angle of arrival (AOA), and received signal strength (RSS) [10]. As the most popular underwater ranging method [11]–[14], TOA is based on the travel time of acoustic signals from source to destination. Synchronized with the source, the destination derives travel time by comparing the received timestamp with its local time. Benefiting from low propagation speed of acoustic signals, TOA methods could achieve high time resolution for impressive ranging accuracy [15]. However, the accuracy comes at the cost of extra hardware requirements, bandwidth occupation, and energy consumption. First, in order to obtain high time resolution, greater precision oscillators and higher sample rate analog to digital converters (ADCs) are required at the physical layer, which increases the manufacture and maintenance expense of sensor nodes. Second, the sensor information transmission efficiency is reduced because of extra messages exchanging for synchronization and ranging, especially in bandwidthlimited underwater acoustic channels (UACs) [1]. For instance, a typical joint synchronization and ranging protocol [16] involves at least four times of communication between sensor nodes. Moreover, the communication overhead may be further aggravated due to the high data error rate of UACs [1]. Third, the service time of UASNs is shortened by extra energy consumption due to extra messages exchanging. Since UASN nodes are usually powered by batteries, they cannot be recharged in time due to seawater corrosion and pressure [17].
在UASN中，测距过程中的物理测量可以通过以下方法之一收集：到达时间（TOA），到达角（AOA）和接收信号强度（RSS）[10]。作为最流行的水下测距方法[11]-[14]，TOA基于声信号从源到目的地的传播时间。与源同步，目的地通过将接收到的时间戳与其本地时间进行比较来得出旅行时间。得益于声学信号的低传播速度，TOA方法可以实现高时间分辨率，从而获得令人印象深刻的测距精度[15]。然而，准确性是以额外的硬件要求、带宽占用和能量消耗为代价的。首先，为了获得高时间分辨率，在物理层需要更高精度的振荡器和更高采样率的模数转换器（ADC），这增加了传感器节点的制造和维护费用。第二，传感器信息传输效率降低，因为额外的消息交换同步和测距，特别是在带宽有限的水声信道（UAC）[1]。例如，典型的联合同步和测距协议[16]涉及传感器节点之间的至少四次通信。此外，由于UAC的高数据错误率，通信开销可能进一步加剧[1]。第三，由于额外的消息交换，UASN的服务时间缩短了额外的能量消耗。由于Udash节点通常由电池供电，由于海水腐蚀和压力，它们无法及时充电[17]。
Compared with TOA-based ranging techniques, RSS-based methods require neither specific hardware support nor extra energy consumption, making it a promising approach for ranging [18]. Existing RSS-based ranging methods [19]–[23] usually transform the measured RSS into distance value by the Urick transmission loss model [24] (more information about the Urick model is given in section II). However, the performance of RSS-based ranging degrades significantly in multipath-rich underwater environments. The degradation is classified into two aspects: 1) The Urick model is incompetent in multipath scenarios, since it depicts the power loss experienced by an acoustic signal propagating along a single path; 2) As a superposition of signals arrived through multiple paths, RSS fails to distinguish each path’s characteristics. In specific, according to the Urick model, it is expected that the measured RSS decreases monotonically with the distance increases. However, this is impractical because acoustic propagations are affected by the multipath effect in underwater environments. Multipath effect is the phenomenon that signals arrive at the receiver through different paths. Those paths are introduced by reflections at the water surface and bottom as well as refractions caused by temperature and salinity [25]. Different paths contribute to diversely attenuated and phase-shifted signals, which combine at the receiver constructively or destructively depending on signal phases. Consequently, the monotonicity defined by the Urick model between measured RSS and corresponding distance is destroyed. Based on the analysis above, efforts of two aspects can be made to improve the ranging performance: 1) an indicator should be exploited to distinguish multipaths; 2) a precise model should be built to depict the complicated acoustic propagations.
与基于TOA的测距技术相比，基于RSS的测距方法既不需要特定的硬件支持，也不需要额外的能量消耗，这使得它成为一种很有前途的测距方法[18]。现有的基于RSS的测距方法[19]-[23]通常通过Urick传输损耗模型[24]将测量的RSS转换为距离值(关于Urick模型的更多信息在第二节中给出)。然而，在多径丰富的水下环境中，基于RSS的测距性能会显著下降。这种退化分为两个方面：1)Urick模型在多径情况下不适用，因为它描述了声信号沿一条路径传播时所经历的功率损失；2)作为通过多条路径到达的信号的叠加，RSS不能区分每条路径的特征。多径效应是指信号通过不同的路径到达接收端的现象。基于以上分析，可以从两个方面努力提高测距性能：1)开发一个指示器来区分多径；2)建立精确的模型来描述复杂的声传播。
In UASNs, orthogonal frequency division multiplexing (OFDM) is widely adopted to fully utilize the limited bandwidth in UACs [26]–[30]. As a fine-grained physical layer indicator, CSI is extensively applied for channel estimation and equalization to eliminate frequency selective fading caused by multipath effect in OFDM communication systems [31]. Compared with RSS, CSI depicts the amplitude-frequency response on the subcarrier level in the frequency domain and separates multipath components in the time domain [32]. Motivated by these characteristics, we propose a novel ranging method named CSI-based ranging for UASNs (CRUN). In summary, the main contributions of this article are as follows:
在UASN中，广泛采用正交频分复用（OFDM）以充分利用UAC中的有限带宽[26]-[30]。作为细粒度的物理层指示符，CSI被广泛应用于信道估计和均衡，以消除OFDM通信系统中由多径效应引起的频率选择性衰落[31]。与RSS相比，CSI在频域中描述了子载波级别上的幅频响应，并在时域中分离了多径分量[32]。受这些特点的启发，我们提出了一种新的测距方法命名为CSI为基础的测距UASN（CRUN）。概括起来，本文的主要贡献如下：
1)CSI is employed as the power indicator instead of RSS. By modeling CSI measurements of multiple subcarriers as a set of power-loss-based equations, the ranging process under multipath scenarios is defined as a multivariate optimization problem involving parameters of not only line-of-sight (LOS) path but also non-line-ofsight (NLOS) paths. This optimization problem aims to simultaneously accomplish the distance estimation and multipath mitigation tasks.
1)CSI被用作功率指示符而不是RSS。通过将多个子载波的CSI测量建模为一组基于功率损耗的方程，将多径场景下的测距过程定义为不仅涉及视线（LOS）路径而且涉及非视线（NLOS）路径的参数的多变量优化问题。该优化问题旨在同时完成距离估计和多径抑制任务。
2)A threshold-window-based algorithm is proposed to simplify the multivariate optimization problem. In specific, the proposed algorithm extracts relative amplitude attenuations and relative time delays between the LOS path and each of the NLOS paths from CSI. According to the extracted relative amplitude attenuations and time delays, NLOS parameters in the multivariate optimization can be represented by the LOS parameter, which simplifies the multivariate optimization problem to a univariate optimization problem only with respect to the desired LOS distance. Then the simplified problem can be efficiently solved by the gradient descent algorithm.
2)提出了一种基于阈值窗口的多变量优化算法。具体地说，该算法从CSI中提取LOS路径和每个NLOS路径之间的相对幅度衰减和相对时间延迟。根据提取的相对幅度衰减和时延，多变量优化中的NLOS参数可以用LOS参数表示，从而将多变量优化问题简化为仅关于期望LOS距离的单变量优化问题。然后利用梯度下降算法对简化后的问题进行求解。
To evaluate the performance of the proposed CRUN method, comprehensive simulations are performed based on a statistical channel model. Furthermore, lake experiments for CRUN on standard OFDM transceivers are conducted. According to both simulation and experiment results, the proposed CRUN method presents a great superiority in both accuracy and robustness than the traditional RSS-based approaches.
为了评估所提出的CRUN方法的性能，基于统计信道模型进行全面的仿真。此外，湖上的标准OFDM收发器的CRUN进行了实验。仿真和实验结果表明，该方法在准确性和鲁棒性方面均优于传统的基于RSS的方法。
The rest of this article is organized as follows. Section II introduces the basic information about OFDM, CSI, and the Urick model. Then the ranging process is defined as an optimization problem in Section III. Section IV elaborates methodologies for the optimization problem, including the threshold-window-based algorithm. The simulation of CRUN and experimental evaluations are presented in Section V and Section VI respectively. The related work is briefly presented in Section VII, followed by discussion in Section VIII. Finally, conclusions are presented in Section IX.
本文的其余部分组织如下。第二节介绍了OFDM、CSI和Urick模型的基本信息。然后在第三节中将测距过程定义为优化问题。第四节阐述了优化问题的方法，包括基于阈值窗口的算法。第五节和第六节分别介绍了CRUN的模拟和实验评估。第七节简要介绍了相关工作，第八节进行了讨论。最后，结论见第九节。

介绍部分主要讨论了水下声学传感器网络（UASNs）中测距的重要性以及现有测距方法的局限性。其中，提到了使用接收信号强度（RSS）作为距离估计方法的优点，但也指出了在多路径丰富的水 6下环境中存在的挑战。为了克服这些挑战，本文提出了一种新的测距方法：基于通道状态信息（CSI）的测距方法，即CRUN。该方法通过将测得的CSI建模为一组基于功率损耗的方程，将多路径情况下的测距问题转化为多元优化问题，并采用阈值窗口算法来简化问题。介绍部分还提到了对CSI估计的必要性以及如何提取相对幅度衰减和相对时间延迟等参数来简化优化问题。最后，介绍部分总结了CRUN方法在测距精度和鲁棒性方面相对于RSS方法的优势，并提出了对未来研究方向的展望。

II. BASIC INFORMATION

二.基本信息
A. OFDM Underwater Acoustic Communication System
A.OFDM水声通信系统
In high speed underwater acoustic communications, as a multicarrier modulation technique, OFDM is one of the mainstream transmission schemes. In OFDM systems, to fully utilize bandwidth and to realize frequency diversity reception, high speed serialized data stream is converted into low-speed parallel data, then modulated into several quadrature mixed and partially overlapped subcarriers for transmission. A scheme of typical OFDM underwater acoustic communication system [33] is shown in Fig. 1. An OFDM modulator can be implemented as an N-point inverse fast fourier transform (IFFT) on a block of N information symbols chosen from an appropriate signal constellation such as quadrature amplitude modulation (QAM) or phase shift keying (PSK), followed by digital to analog converter (DAC) on the IFFT samples. Multipath effect results in a doubly dispersive channel that exhibits dispersion in both time and frequency domains, which causes ISI and frequency selective fading respectively [34]. To mitigate ISI, cyclic prefix (CP) is introduced into the beginning of each block of N-IFFT coefficients. At the receiver, the received signal is sampled by an ADC. With discarding CP, the linear convolution of the transmitted sequence of IFFT coefficients with the discretetime channel is converted into a circular convolution, hence ISI is completely removed. However, CP fails to eliminate interference within a symbol caused by frequency selective fading, therefore a channel equalizer is supplemented. After that, the FFT operation performs baseband demodulation.
在高速水声通信中，作为一种多载波调制技术，OFDM是主流的传输方案之一。在OFDM系统中，为了充分利用带宽，实现频率分集接收，将高速串行化数据流转换成低速并行数据，然后调制成多个正交混合和部分重叠的子载波进行传输。图1示出了典型的ofdm水声通信系统的一种方案[33]。ofdm调制器可以被实现为对从适当的信号星座中选择的N个信息符号块进行N点快速逆傅立叶变换(IFFT)，然后对IFFT样本进行数模转换器(DAC)。多径效应导致双色散信道在时间域和频域都表现出色散，这分别导致码间干扰和频率选择性衰落[34]。为了减少码间干扰，循环前缀(CP)被引入到每个N-IFFT系数块的开始。在接收端，ADC对接收到的信号进行采样。通过丢弃CP，将发送的IFFT系数序列与离散时间信道的线性卷积转换为循环卷积，从而完全消除了码间干扰。然而，CP不能消除由频率选择性衰落引起的码元内的干扰，因此增加了信道均衡器。之后，FFT运算执行基带解调。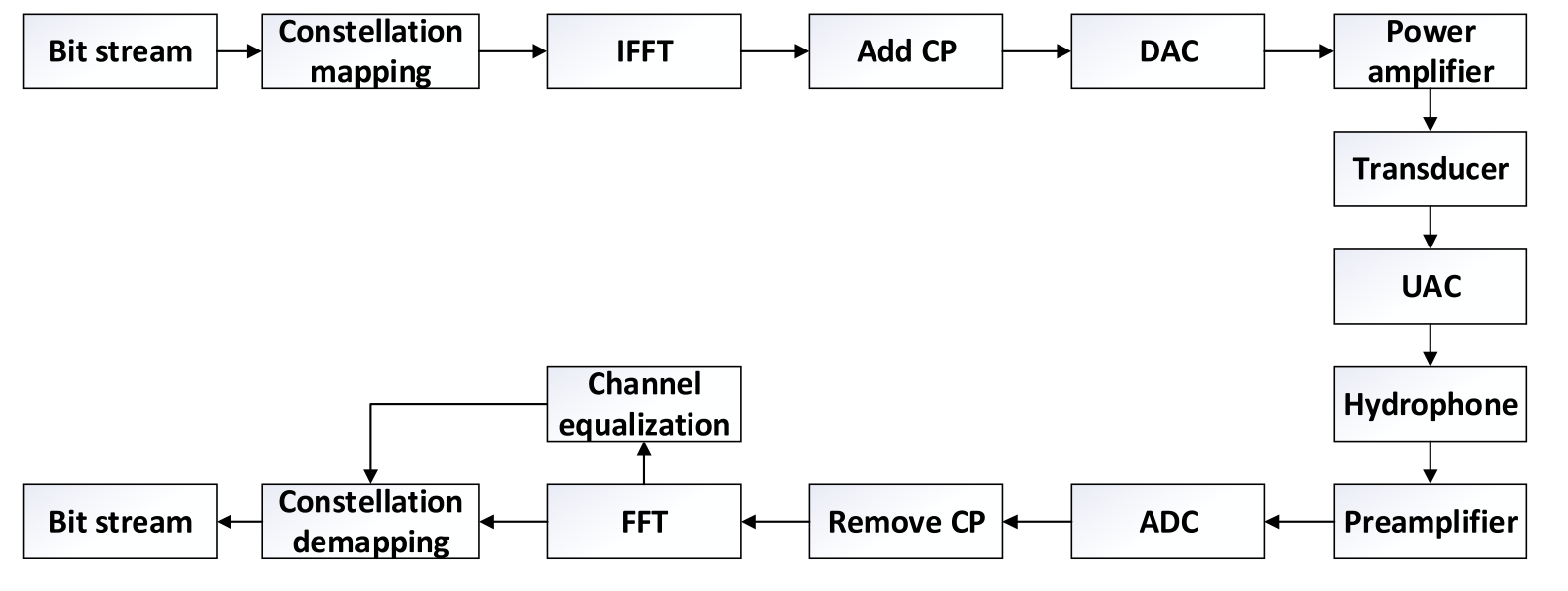

Fig. 1. Block diagram of OFDM underwater acoustic communication system.
图1.ofdm水声通信系统框图。

B. CSI
B. 信道状态信息
In underwater acoustic systems, CSI measurements are applied for channel equalization to improve the reliability of communication. Frequency diversity in OFDM makes CSI measurements on the subcarrier level feasible. CSI describes the attributes of the UACs, which results from a combination of scattering, refraction, reflection, and power attenuation during transmission [35]. In specific, CSI is depicted by channel frequency response (CFR) in the frequency domain and channel impulse response (CIR) in the time domain.
在水声系统中，为了提高通信的可靠性，需要对信道进行CSI测量。频率分集技术使得在子载波级进行CSI测量成为可能。CSI描述了UAC的属性，这是由于传输过程中的散射、折射、反射和功率衰减的组合造成的[35]。具体地，CSI由频域中的信道频率响应(CFR)和时域中的信道冲激响应(CIR)来描述。
In the frequency domain, the constructive and destructive phases cause frequency selective fading, which is characterized as CFR, can be modeled as
在频域中，相长相位和相消相位引起频率选择性衰落，其特征在于CFR，可以建模为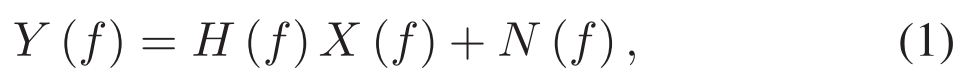

where X (f) and Y (f) are the transmitted and the received signal respectively. H (f) and N (f) are the CFR and the additive white Gaussian noise respectively.
其中X（f）和Y（f）分别是发送信号和接收信号。H（f）和N（f）分别是CFR和加性白色高斯噪声。
Thus, CFR can be estimated according to (1) as

‘Basic Information’部分主要介绍了文章的基本背景信息和相关的技术背景。文章提出了在水下声学传感器网络（UASNs）中进行测距的问题，并指出接收信号强度（RSS）是一种常见的测距方法。然而，由于水下环境的多径传播问题，RSS测距方法存在一定的限制。为了解决这些限制，文章引入了基于通道状态信息（CSI）的测距方法。该方法利用CSI作为测距的指示器，通过将测得的CSI建模为一组基于功率损耗的方程，将测距问题转化为多元优化问题。文章还介绍了采用阈值窗口算法来简化优化问题的过程。此外，文章还讨论了CSI测距方法在水下声学传感器网络中的应用和挑战，并介绍了一些相关的术语和技术背景信息。此部分的目的是为读者提供所需的基础信息，以理解接下来的研究内容。

III. PROBLEM DEFINITION

‘Problem Definition’部分阐述了本文研究的问题定义。文章指出，虽然接收信号强度（RSS）测距方法在水下声学传感器网络（UASNs）中有潜力，但由于水下环境的多路径传播，导致RSS测距方法的准确性受到影响。因此，需要开发一种更准确的测距方法来应对这些挑战。
在多路径环境中，测距问题变得复杂，因为存在许多未知变量。其中的关键问题包括：路径数量未知、非直射路径（NLOS）存在多余的未知变量以及最优解取决于常数C。为了解决这些问题，该文提出了一种基于通道脉冲响应（CIR）的测距方法，并利用CIR的相对参数来简化多元优化问题。
该部分还讨论了如何计算CIR的幅度，以及如何提取相对幅度和时间延迟参数。通过使用CIR估计和提取这些参数，将多元优化问题简化为只涉及所需LOS距离的单变量优化问题。
总的来说，’Problem Definition’部分明确了该文研究的问题，即在水下声学传感器网络中，如何应对多路径传播对测距准确性的影响，并介绍了使用基于CIR的测距方法来解决这一问题的思路。

GPT解读

1. 介绍了基于信道状态信息(channel state information, CSI)的水声传感器网络测距的概念。本节解释了基于接收信号强度(received signal strength, RSS)的测距在多径丰富的水下环境中的局限性，并建议使用CSI作为电源指示器。本文描述了使用CSI测量的测距过程，并提出了涉及视距(LOS)和非视距(NLOS)路径参数的多元优化问题。为了简化优化问题，提出了一种基于阈值窗口的算法来提取LOS路径到NLOS路径的相对幅度衰减和时间延迟。这将问题简化为所需LOS距离的单变量优化问题。文章还讨论了基于csi的测距相对于传统的基于rss的测距的优势，包括提高了精度和鲁棒性。本文的其余部分将提供所提出的方法、模拟和实验评估的进一步细节。
2. 在本节中，作者讨论了解决水声传感器网络(UASNs)优化问题背后的挑战和动机。他们确定了三个主要挑战:未知的路径数量，大量的未知变量，以及最优解的非唯一性。为了简化该问题，作者提出使用信道冲激响应(channel impulse response, CIR)来提取视距(line-of-sight, LOS)路径和每个非视距(non-line-of-sight, NLOS)路径之间的相对幅度衰减和相对时间延迟。他们定义了这些相关参数，并解释了如何从CIR测量中获得这些参数。此外，作者还讨论了未知常数C的确定及其与发射和接收增益的关系。基于这些初步结论，作者提出多变量优化问题可以简化。他们描述了估计CIR和提取相关参数的方法。最后讨论了CIR估计及其与优化问题的关系。
3. 在本节中，作者讨论了CIR估计以及提取信道中每条路径的幅度和时间延迟所涉及的挑战。他们解释说，成形滤波器和带通滤波器的使用会引入噪声并使CIR估计失真。他们提出了一种基于阈值窗口的算法从CIR估计中提取多径参数。他们还讨论了确定优化问题中未知常数C的两种方法，消声坦克训练和在线训练。最后，将优化问题简化为关于距离参数d1的单变量优化问题，并讨论了求解单变量优化问题的一些一般信息。
4. 本节讨论使用梯度下降算法最小化函数(24)的过程。它提到，基于观察，唯一的局部极值是全局最小值的假设通常是有效的。分析了CRUN算法的克拉美劳下界(Cramer-Rao lower bound, CRLB)，并通过仿真实验评估了CRUN算法的性能。研究了距离、噪声方差、子载波数、信噪比等因素对CRUN性能的影响。实验结果表明，CRUN比基于rss的方法具有更高的准确性和鲁棒性，并且即使在传播路径数和信噪比变化的情况下，其性能也保持稳定。本节还简要介绍了CRUN在定位中的评估，并将其与四种基于rss的定位算法进行了比较。
5. 本节概述实验设置和研究中使用的硬件。它提到了实验的地点和所使用的设备的规格。本节还讨论了实验结果，比较了CRUN和基于rss的方法的性能。文中指出，CRUN在准确性和鲁棒性方面始终优于基于rss的方法。本节进一步讨论了室内定位研究与水下定位的相关性，因为这两种环境在拒绝gps和多路径丰富方面有相似之处。介绍了建立测量CSI与距离之间关系的各种现有方法，如基于指纹和基于模型的方法。强调了这些方法的优点和局限性。本节介绍了LiFS，一项利用CSIs在“干净”子载波上进行精确定位的相关工作。它比较了LiFS和CRUN，表明CRUN利用了所有子载波，而LiFS排除了一些子载波。还提到了两种方法用于解决优化问题的不同方法。讨论了在水下环境中实现CRUN的一些挑战和约束，如水声信道的非线性和时变特性。本节提到了研究中为应对这些挑战所采取的措施。文中还指出了CRUN中结合幅度和相位信息的潜力是未来的研究方向。最后，与传统的基于rss的方法相比，CRUN在提高测距精度和鲁棒性方面具有优势。指出细粒度物理层指示CSI和频率分集技术的能力是影响CRUN性能的因素。本节最后提到了未来研究的重点，即进一步改进CRUN。
6. 本节讨论sinc函数第一个旁瓣振幅的计算。它解释了通过确定sinc函数的一阶导数，我们可以找到函数的极值，它表示第一个副瓣的振幅。该剖面给出了一阶导数的方程，并对其进行数值求解以获得极值。然后参照表II介绍测量向量QCSI，它代表不同频率下信道响应的观测值。描述了QCSI的方程，并提到了测量噪声，假设测量噪声是独立同分布的高斯随机变量。推导了QCSI的概率密度函数(probability density function, PDF)，并计算了其对数。为了简化导数计算，截面做了三个假设:1)只考虑视距路径，2)假设球面扩展，3)假设所有子载波的吸收系数是相同的。PDF的对数的一阶导数就是基于这些假设推导出来的。然后介绍费舍尔信息(Fisher information)，它量化了测量提供的关于被估计参数的信息量。通过计算Fisher信息，推导出估计距离参数时可达到的最小方差的克拉美罗下界(CRLB)。最后给出了包含测量噪声方差、距离参数、子载波中心频率和子载波个数的CRLB计算公式。