【学习路线图】深度学习从入门到入土

Channel State Information Prediction for Adaptive Underwater Acoustic Downlink OFDMA System: Deep Neural Networks Based Approach
基于深度神经网络的自适应水声下行OFDMA系统信道状态信息预测

Abstract

In underwater acoustic (UWA) adaptive communication system, due to time-varying channel, the transmitter often has outdated channel state information (CSI), which results in low efficiency. UWA channels are much more difficult to estimate and predict than terrestrial wireless channels, given the more severe multipath environments with varying propagation speeds in different locations, non-linear propagation paths, several-order higher propagation latency, mobile transceiver and obstacles in the sea, etc. To handle the complexity, this paper proposes an efficient online CSI prediction model for UWA CSI prediction considering the complicated correlationship of UWA channels in both the time and frequency domains. This paper designs a learning model called CsiPreNet, which is an integration of a one-dimensional convolutional neural network (CNN) and a long short term memory (LSTM) network. The performance is compared with the widely used recursive least squares (RLS) predictor, the approximate linear dependency recursive kernel least-squares (ALD-KRLS), and two common conventional deep neural networks (DNN) predictors, i.e., back propagation neural network (BPNN) and LSTM network using the measured data recorded in the South China Sea. To validate the efficacy of prediction, we investigate the prediction of CSI in simulated downlink UWA orthogonal frequency division multiple access (OFDMA)systems. Specifically, themeasuredUWA channel is used in the OFDMA system. A joint subcarrier-bitpower adaptive allocation scheme is used for resource allocation. To further improve the performance, we develop an offline-online prediction scheme, enabling theprediction results tobemore stable. Simulation and experimental results show that the CsiPreNet has superior performance than the existing solutions, thanks to its capability in capturing both the temporal and frequency correlation of the UWA CSIs.
在水声（UWA）自适应通信系统中，由于信道的时变特性，发射端往往具有过时的信道状态信息（CSI），导致系统效率低下。考虑到在不同位置具有不同传播速度的更严重的多径环境、非线性传播路径、几阶更高的传播延迟、移动的收发器和海中的障碍物等，UWA信道比陆地无线信道更难以估计和预测。摘要针对水声信道在时域和频域上的复杂相关性，提出了一种有效的水声信道状态信息在线预测模型。本文设计了一种称为CsiPreNet的学习模型，它是一维卷积神经网络（CNN）和长短期记忆（LSTM）网络的集成。性能与广泛使用的递归最小二乘（RLS）预测器，近似线性依赖递归核最小二乘（ALD-KRLS）和两种常见的常规深度神经网络（DNN）预测器进行了比较，即，利用南海实测数据，对BP神经网络（BPNN）和LSTM网络进行了仿真研究。为了验证预测的有效性，我们研究了信道状态信息的预测在下行链路的模拟水声正交频分多址（OFDMA）系统。具体地，在OFDMA系统中使用所测量的UWA信道。一个联合的子载波比特功率自适应分配方案用于资源分配。为了进一步提高预测性能，我们提出了离线-在线预测方案，使预测结果更加稳定.仿真和实验结果表明，CsiPreNet具有比现有方法更优越的上级性能，这要归功于它能够同时捕获水声CSI的时间和频率相关性.
Index Terms—Underwater acoustic (UWA) channel, adaptive communication system, channel state information (CSI)prediction, deep neural network (DNN), orthogonal frequency division multiple access (OFDMA).
索引词——水下声学（UWA）信道，自适应通信系统，信道状态信息（CSI）预测，深度神经网络（DNN），正交频分多址（OFDMA）。

I. INTRODUCTION

Due to the low speed of sound propagation underwater (about 1500 m/s), limited bandwidth, serious multipath and Doppler effects, etc., underwater acoustic (UWA) channels are one of the most challenging communication media [1]. Specifically, UWA channels exhibit larger time dispersions (on the order of hundreds of milliseconds), several-order higher than those with terrestrial radio channels. As such, UWA channels often experience severe inter symbol interference, which requires sophisticated and computationally expensive equalization techniques [2], [3]. Moreover, small-scale phenomena, e.g., scattering caused by surface waves, also contribute to the fast temporal variability of UWA channels [4]. Time-varying multipath propagation and limited bandwidth severely affect the performance of the UWA communication system. To improve spectrum utilization, adaptive communication technology is applied to UWA communication system [5]–[10].
由于声在水下传播速度较低（约1500 m/s）、带宽有限、多径和多普勒效应严重等原因，水声信道是最具挑战性的通信介质之一。具体而言，UWA信道表现出更大的时间分散（数百毫秒的数量级），几阶高于地面无线电信道。因此，UWA信道经常经历严重的符号间干扰，这需要复杂且计算昂贵的均衡技术[2]、[3]。此外，小规模的现象，例如，由表面波引起的散射也有助于UWA信道的快速时间变化[4]。时变多径传播和有限带宽严重影响了水声通信系统的性能。为了提高频谱利用率，自适应通信技术被应用于水声通信系统[5]-[10]。
The performance of the adaptive communication systems depend on the knowledge of channel state information (CSI) provided by the feedback of the receiver. Specifically, CSI determines the physical-layer parameters and setting of adaptive UWA communications. For example, the transmitter needs to implement low-order modulation schemes at the physical layer in the case of poor channel status, and vice versa. Obviously, inaccurate CSI can lead to improper modulation schemes which in turn leads to lowcommunication efficiency. Furthermore, CSI also has a significant impact on resource allocation [11]–[13] in adaptive UWA orthogonal frequency division multiple access (OFDMA) systems. Therefore, obtaining accurate CSI is important for improving the performance of the adaptive UWA communication systems.
自适应通信系统的性能依赖于接收机反馈的信道状态信息（CSI）。具体地，CSI确定自适应UWA通信的物理层参数和设置。例如，在信道状态差的情况下，发射机需要在物理层实现低阶调制方案，反之亦然。显然，不准确的CSI会导致不适当的调制方案，这反过来又会导致通信效率低下。此外，CSI还对自适应UWA正交频分多址（OFDMA）系统中的资源分配具有显著影响[11]-[13]。因此，获得准确的CSI对于提高自适应水声通信系统的性能具有重要意义。
However, because of the large propagation delay and rapid changing of UWA channel, CSI received by the transmitter is usually outdated. Especially, in the UWA communication networks, the central node needs to take more time to obtain the CSIs from all users. This makes the problem of outdated CSI even more severe. In recent years, many researches have studied the performance of adaptive UWA communication systems using outdated CSI. In [14], an adaptive UWA communication scheme for multiantenna transmissions based on the partial CSI was proposed. In [12], long-term statistics of CSI were considered for channel feedback to mitigate the impact of outdated CSI. In [13], the CSI used for feedback was selected between instantaneous CSI and average CSI for system performance improvement. In addition to the extensive research on how to deal with the negative impact of the outdated CSIs, it is found that channel prediction is a desirable method to fully address the problem. Since the speed of sound is very low, the ability to predict the CSI at least one transmission round ahead highly affects the performance of the adaptive communication systems. It is indeed challenging forUWAcommunications in the range of several kilometers, which significant limits the use of feedback.
然而，由于水声信道的传播时延大、变化快，发射端接收到的信道状态信息往往是过时的。特别是在水声通信网络中，中心节点需要花费更多的时间来获得来自所有用户的CSI。这使得过时的CSI问题更加严重。近年来，许多研究都在研究使用过时CSI的自适应水声通信系统的性能。在[14]中，提出了一种基于部分CSI的用于多天线传输的自适应UWA通信方案。在[12]中，信道反馈考虑了CSI的长期统计，以减轻过时CSI的影响。在[13]中，在瞬时CSI和平均CSI之间选择用于反馈的CSI，以改善系统性能。除了对如何处理过时CSI的负面影响进行了广泛的研究之外，还发现信道预测是完全解决该问题的理想方法。由于声音的速度非常低，因此在至少一个传输回合之前预测CSI的能力高度影响自适应通信系统的性能。在几公里范围内的UWA通信确实具有挑战性，这大大限制了反馈的使用。
With a reasonable tracking ability and simple design, a linear predictor applying the recursive least-squares (RLS) algorithm has been widely used for UWA channel impulse responses (CIRs) prediction [8], [15]–[18]. For seasonal UWA time-varying channels, autoregressive (AR) processs [20] and Holt-Winters [21], [24] were introduced to model the seasonal correlation. An efficient adaptive predictor operating in the delay-Doppler domain for UWA time-varying channels was proposed in [25], which does not require any prior knowledge of channel dynamic model and noise statistics.
采用递归最小二乘（RLS）算法的线性预测器具有合理的跟踪能力和简单的设计，已被广泛用于UWA信道脉冲响应（CIR）预测[8]，[15]-[18]。对于季节性UWA时变信道，引入自回归（AR）过程[20]和Holt-Winters [21]，[24]来模拟季节相关性。在[25]中提出了一种用于UWA时变信道的在延迟-多普勒域中操作的有效自适应预测器，其不需要信道动态模型和噪声统计的任何先验知识。
For adaptive UWA OFDM and OFDMA systems, existing channel predictors were often realized at several significant channel taps in the time domain [8], [17]–[19]. Few researchers applied the predictor to each OFDM subcarrier in the frequency domain. This is because the variation at each subcarrier is a combined variation of multiple taps, which makes it difficult to predict using a linear predictor. Moreover, prediction on a large number of OFDM subcarriers leads to high complexity. The traditional linear predictor can not handle frequency domain prediction well. Kernel adaptive filtering (KAF) methods are rapidly gaining popularity to solve a wide variety of prediction, identification and regression problems, since they provide stateof-the-art performance in many real-world applications [22]. In particular, the kernel RLS (KRLS) algorithm based on the RLS algorithm is one ofthe most popular algorithms inKAF[23], and shows good performance in channel prediction [22]. The rapid development of deep neural networks (DNNs) [26], [27], [31], [32] also makes it possible to perform channel prediction in the frequency domain. As long as there are sufficient data to train the neural network, DNNs can capture the complex correlation between different data in both the time and frequency domains. In the past thirty years, DNNs have been widely applied in wireless communications [28]. Reasonable application of DNNs can effectively optimize wireless communication and network system [29]. DNNs will be an indispensable tool for the design and operation of future wireless communication networks [30]. It convinces us that DNNs will also be promising for future research in UWA communications and networks. In wireless communications, many researches focused on channel prediction based on DNNs [33]–[37]. Although some studies have applied DNNs to UWA communications [38], to the best of our knowledge, no research ever used DNNs for channel prediction in UWA communication systems.
对于自适应UWA OFDM和OFDMA系统，现有的信道预测器通常在时域中的几个重要信道抽头处实现[8]，[17]-[19]。很少有研究者在频域中将预测器应用于每个OFDM子载波。这是因为每个子载波处的变化是多个抽头的组合变化，这使得难以使用线性预测器进行预测。此外，对大量OFDM子载波的预测导致高复杂度。传统的线性预测器不能很好地处理频域预测。核自适应滤波（KAF）方法正在迅速普及，以解决各种预测，识别和回归问题，因为它们在许多现实世界的应用中提供了最先进的性能[22]。特别是，基于RLS算法的核RLS（KRLS）算法是KAF中最流行的算法之一[23]，并且在信道预测中显示出良好的性能[22]。深度神经网络（DNN）的快速发展[26]，[27]，[31]，[32]也使得在频域中进行信道预测成为可能。只要有足够的数据来训练神经网络，DNN就可以在时域和频域中捕获不同数据之间的复杂相关性。在过去的三十年里，DNN已经广泛应用于无线通信[28]。DNN的合理应用可以有效地优化无线通信和网络系统[29]。DNN将成为未来无线通信网络设计和运营不可或缺的工具[30]。它使我们相信，DNN也将在未来的研究在西澳大学的通信和网络。在无线通信中，许多研究集中在基于DNN的信道预测[33]-[37]。虽然一些研究已经将DNN应用于UWA通信[38]，但据我们所知，没有研究将DNN用于UWA通信系统中的信道预测。
UWA channels are much more difficult to predict than terrestrial wireless channels, given the more severe multipath environmentswith varying propagation speeds in different locations, non-linear propagation paths, several-order higher propagation latency, mobile transceiver and obstacles in the sea, etc. The existing CSI prediction approaches, e.g., the RLS/KRLS-based prediction methods, only consider the amplitude of the channel tap, and do not consider the variety of the phase. However, when predicting UWA channel, the variety of channel delay cannot be ignored. In addition, due to the requirement of low power consumption of UWA communication hardware design, its computing power is far less than that of wireless communication system, which makes the traditional CSI prediction approaches not fully applicable for UWA channel prediction. In UWAnetworks, such as the Internet ofunderwater things (IoUT) with extremely large-scale deployment of sensor nodes [39], the above difficulties are more serious. To handle the complexity, in this paper, we propose an DNN-based efficient online CSI prediction model for CSI prediction and study the performance according to measured UWA channels in South China Sea. To validate the efficacy of prediction, we investigate the prediction of the measured channels in the simulated UWA OFDMA system. Furthermore, an offline-online prediction scheme is developed to improve system performance. The main contributions of this paper are three-fold.
考虑到在不同位置具有变化的传播速度、非线性传播路径、几阶更高的传播延迟、移动的收发器和海中的障碍物等的更严重的多径环境，UWA信道比陆地无线信道更难以预测。基于RLS/KRLS的预测方法，只考虑了信道抽头的幅度，没有考虑相位的变化。然而，在预测水声信道时，不能忽略信道时延的变化。另外，由于水声通信硬件设计对低功耗的要求，其计算能力远低于无线通信系统，使得传统的CSI预测方法不能完全适用于水声信道预测。在UWA网络中，例如具有超大规模传感器节点部署的水下物联网（IOUT）[39]，上述困难更为严重。为了处理复杂性，本文提出了一种基于DNN的有效的在线CSI预测模型，并根据在南中国海测量的水声信道进行性能研究。为了验证预测的有效性，我们研究了预测的测量信道在模拟的UWA OFDMA系统。此外，离线-在线预测方案的开发，以提高系统的性能。本文的主要贡献有三个方面。

• We design a learning model called CsiPreNet for UWA CSI prediction, that is a combination of a one-dimensional convolutional neural network (CNN) and a long short term memory (LSTM) network. The proposed CsiPreNet can exploit the complicated frequency-temporal correlationship of UWA channels to conduct the CSI prediction effectively. The prediction performance is evaluated with measured channel data recorded in South China Sea. The proposed CsiPreNet has excellent performance on UWA CSI prediction, based on its ability to capture the information in both the frequency and time domains.
  我们为UWA CSI预测设计了一个名为CsiPreNet的学习模型，它是一维卷积神经网络（CNN）和长短期记忆（LSTM）网络的组合。CsiPreNet可以利用水声信道复杂的频时相关性进行有效的CSI预测。用南海实测航道资料对预报性能进行了评价。建议的CsiPreNet具有优异的性能UWA CSI预测的基础上，它的能力，以捕捉在频域和时域的信息。
• We design a simulated downlink UWA OFDMA system, and investigate the impact of CSI prediction. Specifically, the measured UWA channels are used in the simulated OFDMA system as ground truth. A joint subcarrier-bit-power adaptive allocation scheme is used for resource allocation by using the predicted CSI for feedback.
  本文设计了一个仿真的下行UWA OFDMA系统，并研究了CSI预测对下行UWA OFDMA系统性能的影响。具体地，所测量的UWA信道在仿真的OFDMA系统中被用作地面实况。联合子载波比特功率自适应分配方案用于通过使用用于反馈的预测CSI进行资源分配。
• We design an offline-online prediction scheme to improve the stability of the developed learning models when applying it to the simulated OFDMA system. A large amount of historical CSI is input into the offline part to train the learning models, and the trained model is applied to the online part for CSI prediction. The predicted CSI is used as feedback for resource allocation. Furthermore, we update the training data of the offline part after several transmission rounds to ensure the stability of the learning models. Simulation results demonstrate the superior performance of the proposed offline-online prediction based on CsiPreNet model.
  我们设计了一个离线-在线预测方案，以提高稳定性的开发的学习模型时，将其应用到模拟的OFDMA系统。离线部分输入大量的历史CSI数据对学习模型进行训练，训练后的模型应用于在线部分进行CSI预测。预测的CSI被用作资源分配的反馈。此外，我们在几轮传输后更新离线部分的训练数据，以确保学习模型的稳定性。仿真结果表明，基于CsiPreNet模型的离线-在线预测具有良好的上级性能。

The rest of this paper is organized as follows. Section II introduces the related work. In Section III, we describe the downlink UWA OFDMA system, the UWA channel model, and the measured data recorded in sea test. In Section IV, we propose the BPNN, LSTM, and CsiPreNet predictionmodels. In Section V, we present the joint subcarrier-bit-power allocation scheme, the limited feedback for UWA OFDMA system, and the proposed offline-online prediction scheme. In SectionVI, we analyze the prediction performance of the three DNN prediction models using measured CSI, and apply these three models to the simulated downlink UWAOFDMA system for performance evaluation, and then analyze the computational complexity and the running time of all models, followed by the concluding remarks and further research issues in Section VII.
本文的其余部分组织如下。第二节介绍了相关工作。第三部分介绍了水声OFDMA系统的下行链路、水声信道模型以及海上试验的实测数据。在第四节中，我们提出了BPNN，LSTM和CsiPreNet预测模型。在第五节中，我们提出了联合子载波比特功率分配方案，有限反馈的水声OFDMA系统，并提出了离线在线预测方案。在第六节中，我们使用测量的CSI分析了三种DNN预测模型的预测性能，并将这三种模型应用于仿真的下行UWAOFDMA系统中进行性能评估，然后分析了所有模型的计算复杂度和运行时间，然后在第七节中进行了总结和进一步的研究问题。

II. RELATED WORK

Due to the fast changing nature and the extremely limited bandwidth of the UWA channels, an outdated CSI can lead to severe performance degradation, so accurate channel prediction is critical. Although many scholars have studied channel prediction in terrestrial wireless communications [33]–[37], [40], [41], [43], the prediction of UWA channels has received little attention until recent years [8], [15]–[21], [24], [25].
由于水声信道的快速变化和带宽的限制，过时的CSI会导致性能严重下降，因此准确的信道预测至关重要。虽然许多学者研究了地面无线通信中的信道预测[33]-[37]，[40]，[41]，[43]，但直到最近几年[8]，[15]-[21]，[24]，[25]，UWA信道的预测才得到很少的关注。
The prediction methods are generally divided into two categories, i.e., model-based and non-model-based. The modelbased methods assume that certain knowledge and variation about the channel are known, then the correctly defined model can improve the prediction accuracy. For example, the channel variations and parameters were based on an AR model and tracked by an extended Kalman filter in [40], and it assumed that the channel tap coefficients are uncorrelated. By contrast, in [41], it used the RLS algorithm with a postfilter for channel tracking, and considered the multipath correlation. If the real channel does not match the assumed model, the performance of the above-mentioned methods can not be satisfactory. On the contrary, the non-model-based adaptive prediction methods do not rely on the prior knowledge of the channel. Thus it is more suitable for the real communication systems [8], [15]–[21], [24], [25]. Generally speaking, the adaptive predictors can adaptively track channel variations and adjust itself. Least Mean Square (LMS) andRLS are two widely used adaptive algorithms forCSI prediction [8], [15]–[19], [43]. Compared with LMS algorithm, RLS algorithm has the better tracking ability at the cost of a higher computational complexity [42]. The common method using RLS predictor for time domain prediction is shown in Fig. 1 [18], [43]. However, these studies only considered the variety of channel taps and assumed that the delay of channel taps is stable for a certain period of time.
预测方法一般分为两类，即，基于模型和非基于模型。基于模型的方法假设信道的某些知识和变化是已知的，那么正确定义的模型可以提高预测精度。例如，信道变化和参数基于AR模型，并由[40]中的扩展卡尔曼滤波器跟踪，并且假设信道抽头系数不相关。相比之下，在[41]中，它使用RLS算法和后置滤波器进行信道跟踪，并考虑了多径相关性。如果真实的信道与假设的模型不匹配，上述方法的性能不能令人满意。相反，非基于模型的自适应预测方法不依赖于信道的先验知识。因此它更适合于真实的通信系统[8]，[15]-[21]，[24]，[25]。一般来说，自适应预测器可以自适应地跟踪信道变化并调整自身。最小均方（LMS）和RLS是用于CSI预测的两种广泛使用的自适应算法[8]，[15]-[19]，[43]。与LMS算法相比，RLS算法具有更好的跟踪能力，但计算复杂度较高[42]。使用RLS预测器进行时域预测的常用方法如图1 [18]、[43]所示。然而，这些研究仅考虑了信道抽头的变化，并假设信道抽头的延迟在一定时间内是稳定的。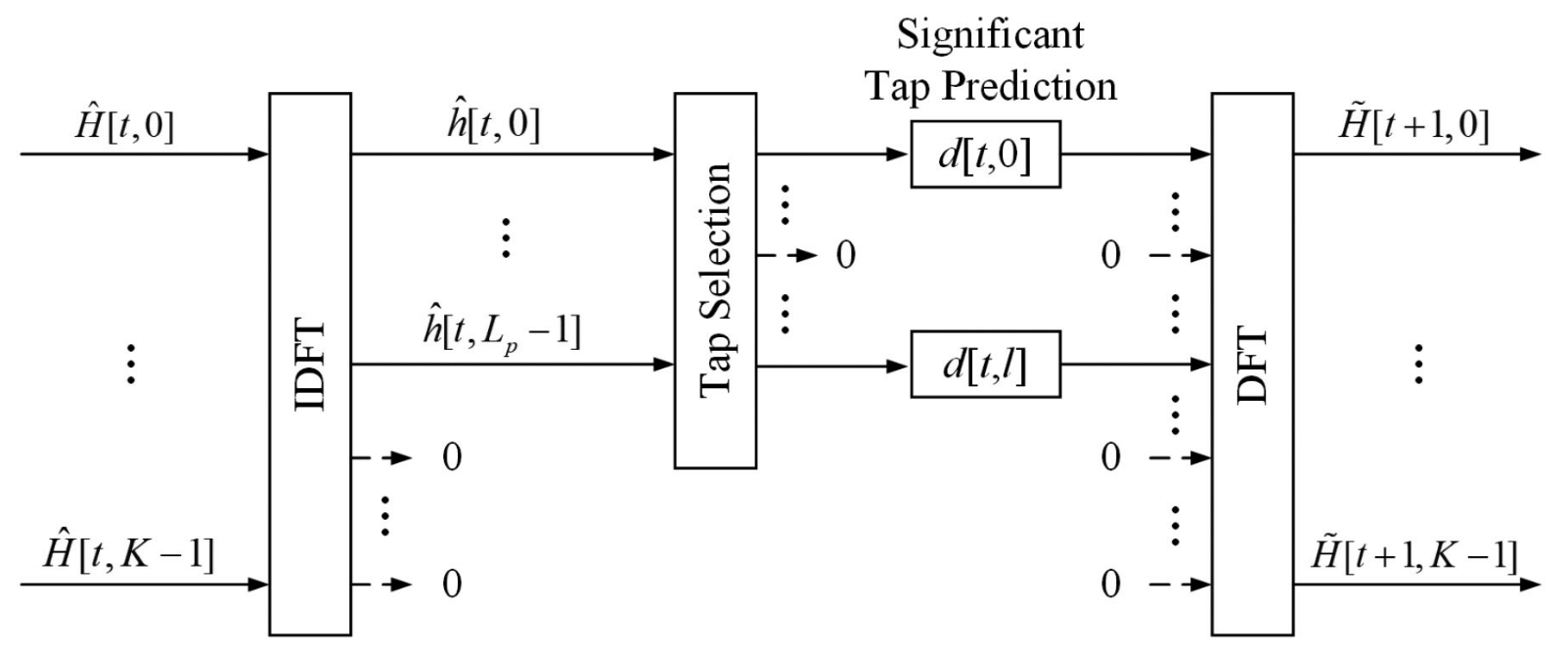

Fig. 1. Time domain predictor for sparse channel based on RLS algorithm.
图1 基于RLS算法的稀疏信道时域预测器。

On the other hand, the rapid development of DNNs makes it possible to capture complex channel variations accurately. In wireless communications, DNNs has been used to predict channel [33]–[37]. It inspires us to apply DNNs to channel prediction inUWA communication systems, which have drastically different channel characteristics.
另一方面，DNN的快速发展使得准确捕获复杂的信道变化成为可能。在无线通信中，DNN已被用于预测信道[33]-[37]。它启发我们将DNN应用于具有截然不同信道特性的UWA通信系统中的信道预测。
Obviously, combining the channel prediction with the adaptive UWA communication system can significantly improve the system performance. In [8], RLS predictor was embedded in an adaptive UWA OFDM system. In [19], a precoding based channel prediction scheme was designed for UWA OFDM system. In [25], the adaptive delay-Doppler spreading function (DDSF) prediction scheme was proposed, and used for UWA communication system under several simulated UWA channels. There is currently no deep learning based prediction model for adaptive UWA communication systems. This work is motivated to fill the gap.
显然，将信道预测与自适应水声通信系统相结合，可以显著提高系统性能。在文献[8]中，RLS预测器被嵌入到自适应UWA OFDM系统中。在[19]中，为UWA OFDM系统设计了一种基于预编码的信道预测方案。在文献[25]中，提出了自适应延迟-多普勒扩展函数（DDSF）预测方案，并将其用于几种模拟水声信道下的水声通信系统。目前还没有用于自适应UWA通信系统的基于深度学习的预测模型。这项工作的动机是填补差距。

III. SYSTEM MODEL AND DATASET DESCRIPTION

三.系统模型和数据集描述
The UWA channel is time-spatial correlated, but in a very complicated way. Due to the characteristics of the long propagation delay (in seconds), curved propagation ray due to different acoustic velocity in different height, relative motions and changing propagation multi-paths, lack of synchronization in UWA channels [1], the parameter design and experiment setup for UWA communication is important.
水声信道具有复杂的时空相关性。由于水声信道具有传播延迟长（秒）、不同高度声速导致的传播射线弯曲、相对运动和传播多径变化、信道不同步等特点，水声通信的参数设计和实验装置非常重要。

A. Downlink UWA OFDMA System
A.下行UWA OFDMA系统
As shown in Fig. 2(a), we consider a simulated downlink UWA OFDMA system with U spatially separated users and a central node.
如图2（a）所示，我们考虑具有U个空间上分离的用户和中心节点的模拟下行链路UWA OFDMA系统。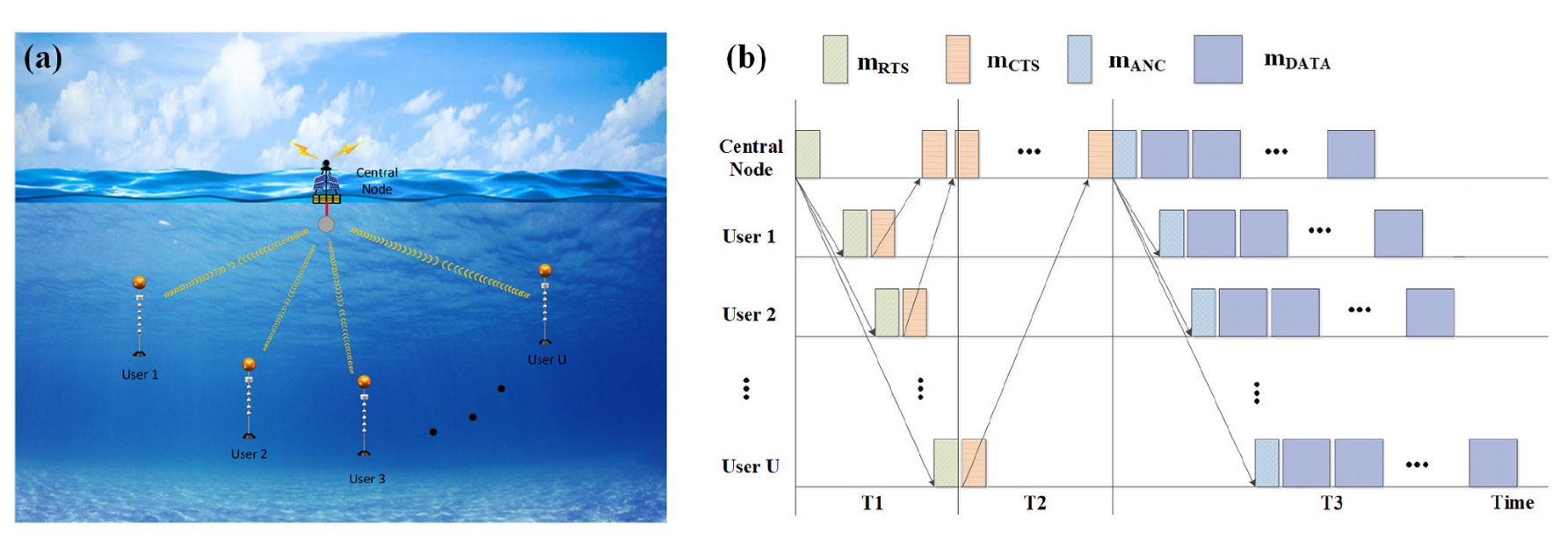

Fig. 2. System model: (a) Downlink UWA OFDMA system, (b) OFDMA handshaking process.
图二 系统模型：（a）下行链路UWA OFDMA系统，（B）OFDMA握手过程。

Consider an OFDMA setup, where a total number of K subcarriers are allocated to all users. $K_u$ non-overlapping subcarriers are allocated to user u, where $\sum_{u=1}^U K_u=K$.The OFDM symbol period is T, the cyclic prefix (CP) length is $T_{c p}$, and the subcarrier interval is 1/T. The center frequency is $f_c$, and then the subcarrier frequency $f_k$ = $f_c$ + k/T, k = −K/2,…,K/2 − 1. Define d[k] as the coded information on the k-th subcarrier, and then the transmitted signal is
考虑OFDMA设置，其中总共K个子载波被分配给所有用户。$K_u$ 个不重叠的子载波被分配给用户u，其中，$\sum_{u=1}^U K_u=K$。OFDM符号周期是T，循环前缀（CP）长度是$T_{c p}$，并且子载波间隔是1/T。中心频率是$f_c$，然后子载波频率$f_k$ = $f_c$ + k/T，k =-K/2，.，K/2 − 1。将d[k]定义为第k个子载波上的编码信息，然后发送的信号为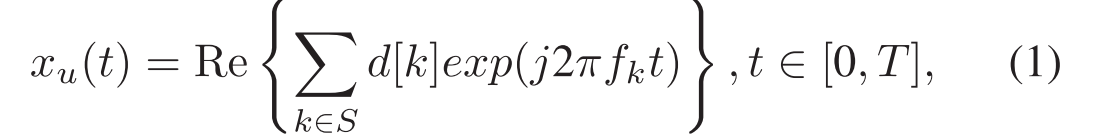

where S is the subcarrier index set, including the data subcarrier index set $S_D$ and the combpilot index set $S_P$, S = $S_D$ ∪ $S_P$. All users use the same pilot symbols for channel estimation, and the k-th subcarrier can only be allocated to one user, where k ∈ $S_D$. The candidate modulation schemes of d[k] are binary phase shift keying (BPSK), quadrature phase-shift keying (QPSK), 8-quadrature amplitude modulation (8QAM),and 16-quadrature amplitude modulation (16QAM) with 2-D Gray mapping. In other words, for the k-th subcarrier, where k ∈ $S_D$, the modulation level $M_K$ ∈{2, 4, 8, 16}, and if no data are transmitted, $M_K$ = 1. We assumed that the pilot symbols (k ∈ $S_P$) use the modulation scheme of QPSK.
其中S为子载波索引集，包括数据子载波索引集SD和梳状导频索引集$S_P$，S = $S_D$ ∪ $S_P$，所有用户使用相同的导频符号进行信道估计，第k个子载波只能分配给一个用户，其中k ∈ $S_D$。d[k]的候选调制方案是具有2-D格雷映射的二进制相移键控（BPSK）、正交相移键控（QPSK）、8正交幅度调制（8 QAM）和16正交幅度调制（16 QAM）。换句话说，对于第k个子载波，其中k ∈ $S_D$，调制级别$M_K$ ∈{2，4，8，16} ，并且如果没有数据被发送，则$M_K$ = 1。我们假设导频符号（k ∈ $S_P$)使用QPSK的调制方案。
Assuming that the receiver (user u) has correctly compensated for the Doppler frequency offset caused by the relative motion, the time-varying UWA multipath channel model transmitted from the central node to user u in a CP-OFDM block can be expressed as
假设接收器（用户u）已经正确地补偿了由相对运动引起的多普勒频率偏移，则在CP-OFDM块中从中心节点发送到用户u的时变UWA多径信道模型可以表示为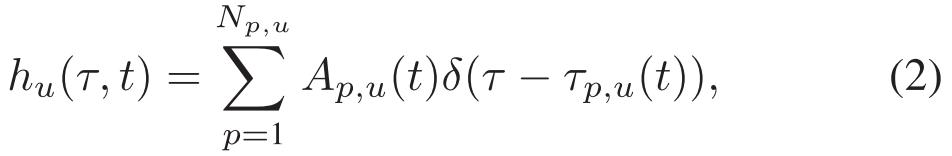

where $N_{p, u}$ is the number of channel paths from the central node to user u; $A_{p, u}(t)$ is the attenuation coefficient of the p-th path in a CP-OFDM block; $T_{p, u}(t)$ is the time delay corresponding to the p-th path. Assuming that the CP length $T_{c p}$ is longer than the maximum multipath delay, the signal received by user u is
其中$N_{p, u}$为中心节点到用户u的信道路径数; $A_{p, u}(t)$``为CP-OFDM块中第p条路径的衰减系数; $T_{p, u}(t)$为第p条路径对应的时延，假设CP长度$T_{c p}$大于最大多径时延，则用户u接收到的信号为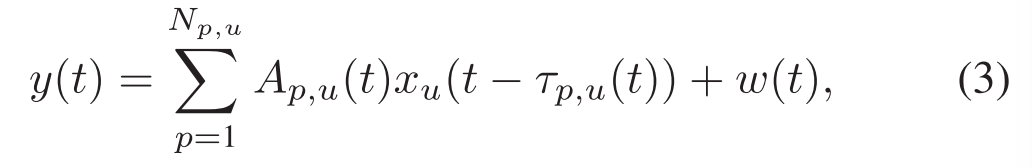![](https://cdn.jsdelivr.net/gh/YangQingHui66/CDN/blog-img/UASN/2-5.png) where w(t) is the additive noise. Substituting (1) into (3), after removing CP and undergoing discrete fourier transform (DFT) transformation, the frequency domain baseband reception vector of user u on the k-th subcarrier can be obtained by其中w(t)是加性噪声。将（1）代入（3），在去除CP并进行离散傅立叶变换（DFT）之后，可以通过下式获得用户u在第k个子载波上的频域基带接收向量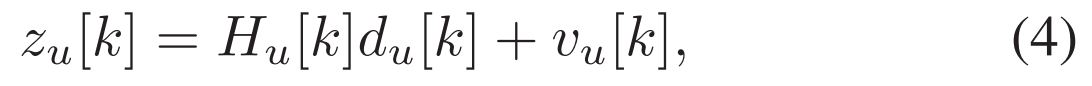：![](https://cdn.jsdelivr.net/gh/YangQingHui66/CDN/blog-img/UASN/2-6.png) where $Z_u[k]$ and $d_u[k]$ represent the received data and the transmitted data on the k-th subcarrier allocated to user u, respectively. $H _u[k]$ represents the channel gain of user u on the k-th subcarrier. $V_u[k]$ is the frequency domain additive noise in the frequency domain. CSI can be measured in the form of Signal-to-noise ratio (SNR), which can be expressed as其中$Z_u[k]$和$d_u[k]$分别表示分配给用户u的第k个子载波上的接收数据和发送数据。$H _u[k]$ 表示用户u在第k个子载波上的信道增益。$V_u[k]$是频域中的频域加性噪声。CSI可以以信噪比（SNR）的形式测量，其可以表示为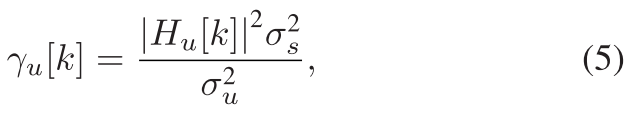![](https://cdn.jsdelivr.net/gh/YangQingHui66/CDN/blog-img/UASN/2-7.png) where $\sigma_s^2$ is the symbol energy, and $\sigma_u^2$ is the noise variance of user u.其中$\sigma_s^2$是符号能量，$\sigma_u^2$是用户u的噪声方差。Therefore, based on the knowledge of the transmitted and received signals, i.e., d[k] and z[k], the CSI can be estimated. So far, scholars have developed several CSI estimation methods, e.g., maximum likelihood (ML), minimum mean square error (MMSE), least squares (LS), and compressed sensing (CS) methods. In this paper, we use the orthogonal matching pursuit (OMP) algorithm [44] for CSI estimation, which is one of the CS methods.因此，基于对所发送和接收的信号的了解，即，d[k]和z[k]，可以估计CSI。到目前为止，学者们已经开发了几种CSI估计方法，最大似然（ML）、最小均方误差（MMSE）、最小二乘（LS）和压缩传感（CS）方法。在本文中，我们使用正交匹配追踪（OMP)算法[44]进行CSI估计，这是CS方法之一。Furthermore, the handshaking process of this adaptive downlink UWA OFDMA system is shown in Fig. 2(b). The CSI of each user is estimated by the request-to-send (RTS) packet, and then embedded into the clear-to-send (CTS) packet. The central node collects all users’ CSIs, and performs the adaptive resource allocation scheme based on them. Furthermore, the allocation table is embedded in the announcement (ANC) packet, and broadcasted with the DATA packet to all users. Upon reception, each user decodes its own data based on the allocation table. Therefore, the CSI embedded in a CTS packet is the CSI based on the RTS packet in slot T1, which outdates while using it for resource allocation in slot T3, under time-varyingUWAchannel.此外，图2（B）示出了该自适应下行链路UWA OFDMA系统的握手过程。每个用户的CSI通过请求发送（RTS）分组估计，然后嵌入到清除发送（CTS）分组中。中心节点收集所有用户的CSI，并根据它们执行自适应资源分配方案。此外，分配表被嵌入在通知（ANC）分组中，并且与DATA分组一起被广播给所有用户。在接收时，每个用户基于分配表解码其自己的数据。因此，在时变UWA信道下，嵌入在CTS分组中的CSI是基于时隙T1中的RTS分组的CSI，其在用于时隙T3中的资源分配时过时。`

Fig. 2. System model: (a) Downlink UWA OFDMA system, (b) OFDMA handshaking process.
图二 系统模型：（a）下行链路UWA OFDMA系统，（B）OFDMA握手过程。

B. Experimental Dataset Description
B.实验数据集描述
We carried out the sea trial in Lingshui Bay, South China Sea on May 8, 2014. In the experiment, two ships were used for communication. The sea depth was 70 meters. One ship was the transmitter with a transducer deployed 27 meters depth. Another ship was the receiver with a four-element line array deployed at the depth of 30 meters, and array element spacing was 0.6 meters. Transmission distance ranged from 1 km to 5 km. The geometry ofthe experiment and the setup ofthe system are given in Fig. 3(a).
我们于2014年5月8日在南海陵水湾进行了海试。在实验中，两艘船被用于通信。海深70米。一艘船是发射器，其换能器部署在27米深的地方。另一艘是接收船，四元线阵，部署在30米深，阵元间距0.6米。传输距离从1公里到5公里不等。实验的几何形状和系统的设置如图3（a）所示。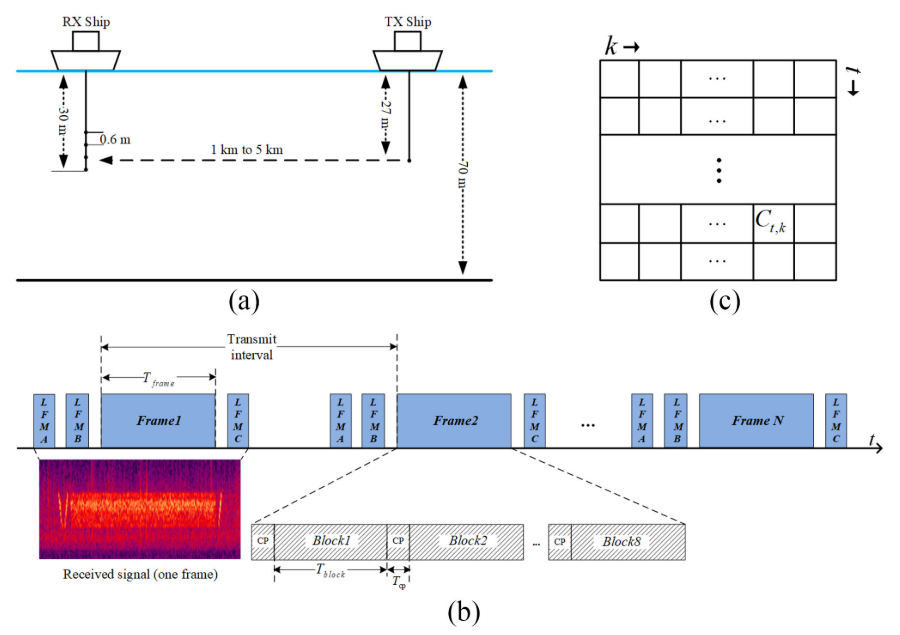

Fig. 3. Experimental setup: (a) The geometry and the setup of the communication system. (b) Structure of one frame OFDM signal. (c) Organized CSI image.
图三 实验装置：（a）通信系统的几何形状和装置。(b)一帧OFDM信号的结构。(c)有条理的犯罪现场调查。

As shown in Fig. 3(b), the transmitter sends frames of CPOFDM blocks. Each frame contains 8 OFDM blocks. One OFDM block has 681 subcarriers, which contains 595 data subcarriers and 86 pilot subcarriers, and the pilot interval is 8. CSI is estimated from the pilot subcarriers. CP length, block length and frame length areTcp=25 milliseconds (ms),Tblock=171 ms, and Tframe=1.568 seconds (s), respectively. The transmission interval between two adjacent frames is 4 s. The bandwidth is 4 kHz (kHz), and the central frequency is 8 kHz. LFM A signal is used for signal synchronization, whileLFMB signal andLFM C signal are the same signal that are used for Doppler estimation.
如图3（B）所示，发射机发送CPOFDM块的帧。每个帧包含8个OFDM块。一个OFDM块具有681个子载波，其包含595个数据子载波和86个导频子载波，并且导频间隔为8。从导频子载波估计CSI。CP长度、块长度和帧长度分别为Tcp =25毫秒（ms）、Tblock=171 ms和Tframe=1.568秒（s）。两个相邻帧之间的传输间隔为4s。带宽为4 kHz（kHz），中心频率为8 kHz。LFM A信号用于信号同步，而LFMB信号和LFM C信号是用于多普勒估计的相同信号。

Fig. 3. Experimental setup: (a) The geometry and the setup of the communication system. (b) Structure of one frame OFDM signal. (c) Organized CSI image.
图三 实验装置：（a）通信系统的几何形状和装置。(b)一帧OFDM信号的结构。(c)有条理的犯罪现场调查。

The channel of each block can be estimated by the pilot signal in the block. The time interval between two channels of the same block in adjacent frames is 4 s. We record a large amount of measured UWA CSI. We organize the CSI into a two-dimensional image as shown in Fig. 3(c). One dimension is the frequency dimension, representing the k-th subcarrier, and another dimension is the time dimension, representing the time t.
每个块的信道可以通过该块中的导频信号来估计。相邻帧中同一块的两个通道之间的时间间隔为4s。我们记录了大量测量的UWA CSI。我们将CSI组织成如图3（c）所示的二维图像。一个维度是频率维度，表示第k个子载波，另一个维度是时间维度，表示时间t。

Fig. 3. Experimental setup: (a) The geometry and the setup of the communication system. (b) Structure of one frame OFDM signal. (c) Organized CSI image.
图三 实验装置：（a）通信系统的几何形状和装置。(b)一帧OFDM信号的结构。(c)有条理的犯罪现场调查。

We can also express the CSI image as a matrix
我们还可以将CSI图像表示为矩阵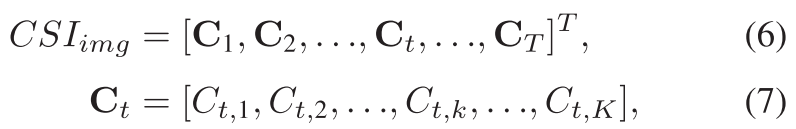

where $C_{t, k}$ represents the CSI of the k-th subcarrier at the time t.
其中$C_{t, k}$表示在时间t的第k个子载波的CSI。
This paper selects two different measured channels with a transmission distance of 3 km and 5 km for analysis. In this case, the two ships anchored at a distance of 3 km and 5 km, respectively. But the ships still drift randomly in a small range with the water surface waves, resulting in time-varying of the channel. The analytical results will be presented in Section VI.
本文选取了传输距离为3 km和5 km的两个不同的实测信道进行分析。在这种情况下，两艘船分别在3公里和5公里的距离抛锚。但船舶仍随水面波在小范围内随机漂移，导致航道时变性。分析结果见第VI节。

IV. PREDICTION MODEL BASED ON DNN

四.基于DNN的预测模型
The long propagation delay makes it critical to conduct accurate channel prediction, while the complicated mobile UWA environment makes the traditional solutions less effective. Therefore, we investigate the deep-learning approach for UWA channel prediction.
长传播时延使得进行准确的信道预测变得至关重要，而复杂的移动的水声环境使得传统的解决方案效果不佳。因此，我们研究了用于UWA信道预测的深度学习方法。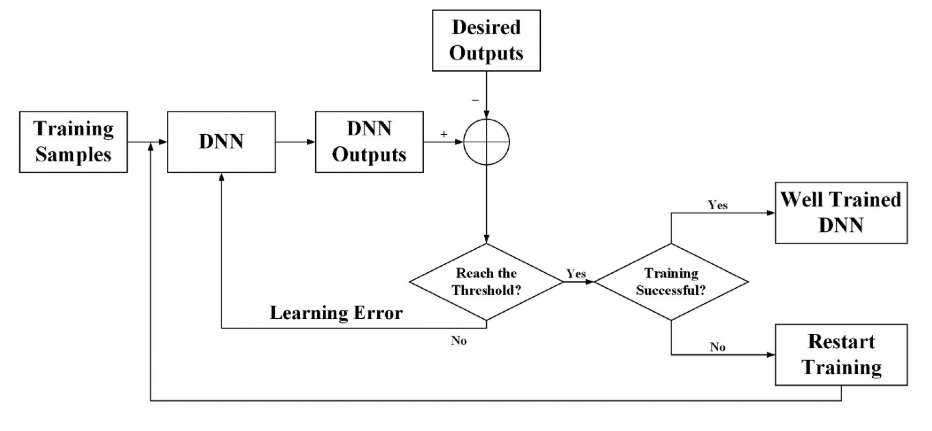

In this section, we will introduce three DNN models, i.e., BPNN, LSTM, and the proposed CsiPreNet. We use these three models for CSI prediction. Fig. 4 shows the training process of a typic DNN. Generally speaking, a DNN prediction model consists of two parts, the training part and the prediction part. Before the prediction part works, the network must be trained by the training symbols in the training part. First, the training samples are input into the neurons in the hidden layers and then are propagated to the output layer. If the learning errors between the DNN output results and the desired outputs are not reached the training threshold, the learning errors will be back-propagated from the output layer to the hidden layers. Meanwhile, the weights and biases in the neurons will be updated according to the learning errors. The training part will be repeated until the training threshold are reached, such as a given number of training rounds have been completed, or a certain learning error has been met. Finally, the well-trained model is used for CSI prediction.
在本节中，我们将介绍三种DNN模型，即，BPNN、LSTM和CsiPreNet。我们使用这三个模型进行CSI预测。图4示出了典型DNN的训练过程。一般来说，DNN预测模型由两部分组成，训练部分和预测部分。在预测部分工作之前，网络必须由训练部分中的训练符号进行训练。首先，将训练样本输入到隐藏层的神经元中，然后将其传播到输出层。如果DNN输出结果和期望输出之间的学习误差没有达到训练阈值，则学习误差将从输出层反向传播到隐藏层。同时，神经元中的权值和偏置将根据学习误差进行更新。训练部分将重复进行，直到达到训练阈值，例如已经完成给定数量的训练轮，或者已经满足特定的学习错误。最后，训练好的模型用于CSI预测。

A. Back Propagation Neural Network (BPNN)
A.反向传播神经网络
BPNN can be described as a multilayer perceptron (MLP) neural network with multiple hidden layers trained by the back propagation algorithm [45], [46]. Fig. 5 illustrates a typical BPNN, which includes an input layer, multiple hidden layers, and an output layer.
BPNN可以描述为多层感知器（MLP）神经网络，具有通过反向传播算法训练的多个隐藏层[45]，[46]。图5示出了典型的BPNN，其包括输入层、多个隐藏层和输出层。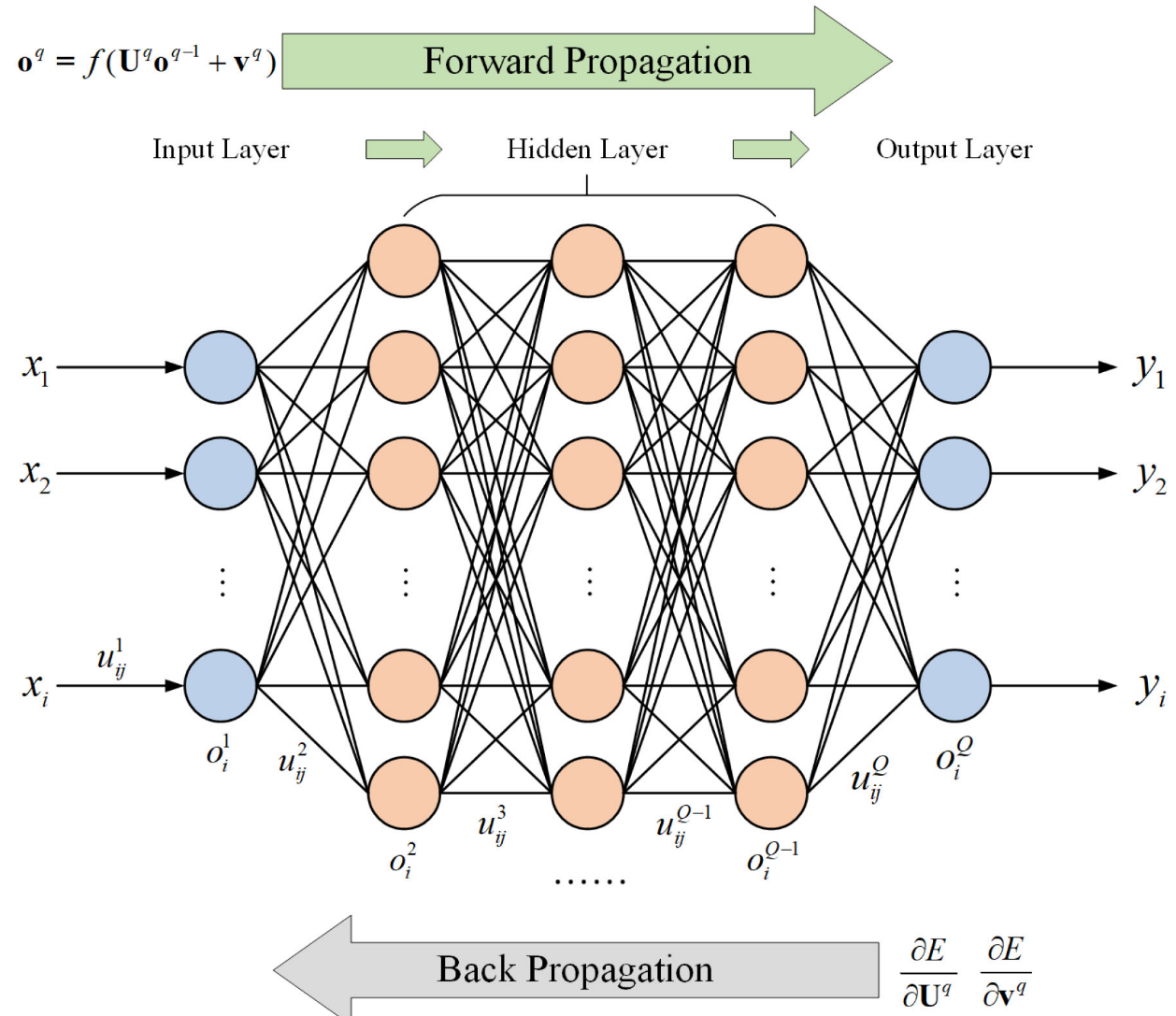

Fig. 5. Typical architecture of BPNN model.
图五 BPNN模型的典型结构。

Then the back propagation algorithm [45], [46] is used to update the weights U and biases v in the neurons according to the learning errors. As shown in Fig. 5, the training part of the BPNN can be summarized as the forward propagation of training symbols and the back propagation of updating errors.
然后使用反向传播算法[45]，[46]根据学习误差更新神经元中的权重U和偏置v。如图5所示，BPNN的训练部分可以概括为训练符号的前向传播和更新误差的反向传播。
The update of BPNN can be briefly summarized as follows
BPNN的更新可以简单地总结如下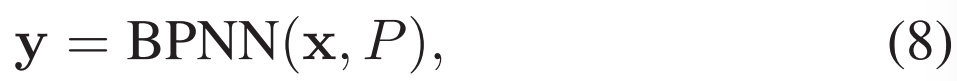

where BPNN(·) presents all propagation process of BPNN, and P represents all the parameters in the BPNN.
其中BPNN(·)表示BPNN的所有传播过程，P表示BPNN中的所有参数。
For the CSI prediction, we replace x and y with $C_t$,$C_{t−1}$,…,$C_{t−n}$ and $C_{t+1}$ defined in (7), respectively. The prediction expression can be expressed as
对于CSI预测，我们用$C_t$,$C_{t−1}$,…,$C_{t−n}$ 和 $C_{t+1}$分别定义在（7）中。预测表达式可以表示为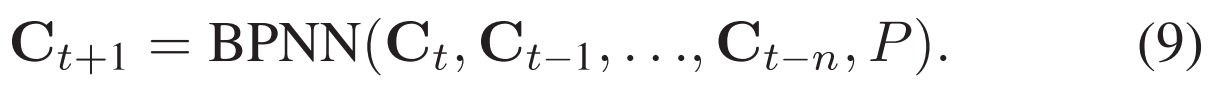

B. Long Short Term Memory (LSTM)
B.长短期记忆（LSTM）
The LSTM network is explicitly designed to handle the long-term dependency problem, which is suitable for time series prediction [48]. LSTM network uses the approximate gradient calculation algorithm, which updates the weight matrices after each time step. However, the back-propagation algorithm can be used to calculate the entire gradient.
LSTM网络被明确设计用于处理长期依赖性问题，这适用于时间序列预测[48]。LSTM网络使用近似梯度计算算法，该算法在每个时间步后更新权重矩阵。然而，反向传播算法可用于计算整个梯度。
In a typical LSTM network, each cell has four gates, interacting in a special way. Fig. 6 illustrates a single LSTM memory cell.
在典型的LSTM网络中，每个单元有四个门，以特殊的方式相互作用。图6示出了单个LSTM存储器单元。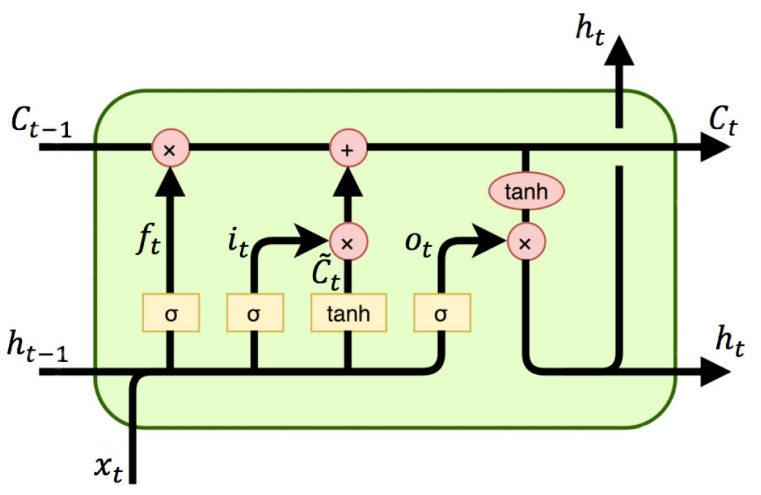

Fig. 6. Typical architecture of LSTM cell.
见图6 LSTM单元的典型架构。

GPT解读

水声通信具有许多独特的特点，主要有以下几个方面：

1. 声传播速度低：在水中，声波的传播速度较低，通常约为1500米/秒，相对于空气中的声速约为4倍。这使得水声通信系统中的信号传输延迟较高。
2. 信道环境复杂：水中存在多种复杂的信道环境，包括多径传播、声波反射、折射和散射等。这些环境特性导致信号在水中传播时会发生衰减、时延扩展和多径干扰等问题。
3. 多径干扰：由于水中存在不同的障碍物和反射面，导致声波在传播过程中经历多条不同路径。这将导致接收到的信号是多径组合的结果，增加了信道估计和信号解调的复杂性。
4. 环境噪声：水中存在各种噪声源，如自然水流、动物、船只等。这些噪声源会干扰通信信号，降低通信系统的性能。
5. 频率损耗：在水中，高频信号的传播损耗比低频信号更大。这意味着在水声通信系统中，需要有针对性地选择合适的频率范围来保证信号的传输可靠性。

总体而言，水声通信由于特殊的传播介质和环境条件，与传统的无线通信系统有很大的差异。在设计水声通信系统时，需要充分考虑水声信道的特点，并采取相应的信号处理和调制技术来提高系统性能和可靠性。

前人研究的方法

1. 递归最小二乘（RLS）预测器：这种方法使用递归最小二乘算法来估计和预测水声信道的状态信息（CSI）。它根据历史观测值和预测误差来更新预测器的权重系数。RLS预测器能够提供高准确性的CSI预测，但在计算复杂度和存储需求方面较高。
2. 基于预编码的方法：这种方法将预编码应用于水声通信中，通过对发送信号进行调制和编码来抵消信号在复杂水声信道中的衰落和干扰。预编码方法可以提供更好的抗干扰能力和传输可靠性，但需要较高的计算资源和功耗。
3. 基于深度学习的方法：前人研究也探索了使用深度学习技术来解决水声信道预测问题。深度学习模型如卷积神经网络（CNN）和长短期记忆（LSTM）神经网络可用于建模和预测复杂的水声信道状态。这些方法可以通过学习频率和时间域上信道的相关性来提高预测性能。

作者要解决的问题

根据这篇文章，作者主要要解决的问题是在水声自适应通信系统中，由于水声信道的时变性，发送方常常面临过时的信道状态信息（CSI），从而降低了系统的效率。由于水声信道相对于陆地无线信道更加复杂，很难准确估计和预测信道状况。因此，作者旨在提出一个有效的在线CSI预测模型，以考虑水声信道在时间和频域中的复杂相关性，从而改善自适应水声通信系统的性能。具体而言，论文的创新点包括设计了一个名为CsiPreNet的学习模型，它是一维卷积神经网络（CNN）和长短期记忆（LSTM）网络的结合。通过结合这两种网络结构，CsiPreNet模型可以捕捉到水声信道在频率和时间域上的复杂关联性，从而实现对CSI的准确预测。此外，论文还提出了离线-在线预测方案，用于改善系统的稳定性，并探讨了不同预测模型的性能比较，以及预测结果对于水声OFDMA系统性能的影响。通过解决这些问题，作者旨在提高水声自适应通信系统的性能，并推动水声通信领域的发展。

作者通过什么样的方法来解决所提出的研究问题

作者通过采用深度神经网络（DNN）的方法来解决所提出的研究问题。具体而言，作者设计了一个名为CsiPreNet的学习模型，它是一维卷积神经网络（CNN）和长短期记忆（LSTM）网络的结合。这种组合的结构能够充分捕捉水声信道在时间和频率域上的复杂相关性。

首先，通过一维CNN模型，CsiPreNet模型可以有效提取相邻子载波之间的频率相关性。通过应用多个滤波器对信道状态信息（CSI）图像进行处理，CNN模型能够计算卷积结果并通过最大池化提取出显著特征。最后，将所有滤波器的输出结果进行组合并展开为一个向量。

然后，通过LSTM模型，CsiPreNet模型能够捕捉到CSI在时间上的相关性。使用这个模型，可以对当前向量进行预测。最后，使用完全连接的softmax层生成预测结果的概率分布。

为了训练CsiPreNet模型，作者使用了在南海收集的实测CSI数据，并对模型进行了参数设置和超参数优化。通过在实验中比较CsiPreNet模型与基于RLS和ALD-KRLS的预测器以及其他DNN模型的性能，作者证明了CsiPreNet模型在准确性方面的优势，并对其性能进行了评估和分析。

综上所述，作者通过设计组合了CNN和LSTM网络的CsiPreNet模型来解决水声通信系统中的CSI预测问题，从而提高了水声自适应通信系统的性能。

作者通过哪些实验得出来了这些结果

作者通过一系列实验来验证他们提出的方法和研究结果。首先，他们使用在南海采集到的水声信道状态信息（CSI）数据集进行了训练和测试。这个数据集包含了在水下环境中记录的真实信道数据。

在实验中，作者比较了不同深度神经网络模型（包括BPNN，LSTM和CsiPreNet）以及基准预测器（RLS和ALD-KRLS）的性能。他们通过测量均方根误差（RMSE）和平均绝对百分比误差（MAPE）来评估预测误差。

此外，作者还通过绘制累积分布函数（CDF）来分析不同模型的预测误差分布情况。他们还考虑了不同参数设置和训练轮数对于模型性能的影响。

为了验证他们的方法对自适应水声通信系统的实际影响，作者还在一个模拟的OFDMA系统中进行了性能评估。他们比较了使用预测CSI和实际CSI进行资源分配的系统效果，以评估预测的准确性和对系统性能的影响。

通过这些实验，作者得出了他们提出的CsiPreNet模型在水声通信系统中预测信道状态信息方面的优越性能，并验证了他们的方法对自适应通信系统的效果。

实验部分的不足

1. 缺乏更大规模的实际水声信道数据集：文章中作者所使用的实验数据集是在南海采集的真实信道数据，但规模相对较小。更多和更广泛的实际数据集可能有助于更全面地评估所提出方法的性能。
2. 缺乏与其他算法的直接比较：文章中对所提出方法的性能进行了比较，但并未直接与其他现有的水声通信信道预测算法进行详细对比。直接与其他方法进行比较可以更好地了解所提出方法的优势和局限性。
3. 缺乏对不同实际环境条件的探索：文章中所选择的实验环境是南海，在其他不同的水下环境条件下，信道特性可能会有所不同。更多针对不同实际环境的实验将有助于验证所提出方法的鲁棒性和适应性。
4. 缺乏性能受到参数选择的检验：在实验中，所提出方法的性能高度依赖于网络结构和参数选择。然而，在文章中并没有进行详细的参数选择实验，这可能导致一些参数的选择不够优化。

综上所述，将来的研究可以通过增加规模更大的实际数据集，与其他现有算法进行直接比较，并在更多的实际环境条件下进行实验来进一步探索所提出方法的优势和不足之处。此外，对网络结构和参数选择进行更多的实验和分析也是一个重要的方向

作者使用该方法的优点

作者使用所提出的方法（CsiPreNet模型）具有以下优点：

1. 高准确性：CsiPreNet模型通过结合一维卷积神经网络（CNN）和长短期记忆（LSTM）网络，能够捕捉水声信道在时间和频域上的复杂相关性。与传统的方法相比，CsiPreNet在水声信道状态信息（CSI）的预测方面表现更为准确。
2. 考虑时变性：水声信道具有时变性，因此需要实时进行CSI的预测。CsiPreNet模型通过在线学习和预测的方式来处理时变信道，使得系统能够及时适应信道变化。
3. 适用性广泛：CsiPreNet模型在实验中展示了在不同信道环境和不同信噪比条件下的高性能。它可以应用于各种水声通信场景，提供更稳定和高效的通信性能。
4. 低计算复杂度：与传统的递归最小二乘（RLS）方法相比，CsiPreNet模型具有较低的计算复杂度。这使得它在实时水声通信系统中具有可行性。

综上所述，作者使用CsiPreNet模型具有高准确性、时变性适应性、广泛适用性和较低计算复杂度等优点，有望提高水声自适应通信系统的性能。

作者使用该方法的缺点

根据文章内容，以下是作者使用该方法（CsiPreNet模型）的一些可能的缺点：

1. 训练复杂度高：文章中提到，训练DNN模型（包括CsiPreNet模型）的过程具有较高的计算复杂度。这可能需要大量的训练时间和计算资源。
2. 参数调节：CsiPreNet模型的性能可能受到参数调节的影响。找到最佳的模型参数和超参数（如网络深度、神经元数量等）需要一定的经验和实验调节。
3. 数据需求量大：DNN模型通常需要较大规模的数据集进行训练，以获得良好的性能。在实际应用中，获取足够数量和质量的水声信道数据可能具有挑战性。

请注意，以上缺点是根据对文章内容的理解进行的推测，具体的缺点可能需要进一步的研究和验证。

论文的创新点主要体现在以下几个方面：

1. 水声信道状态信息（CSI）的预测模型：论文提出了一种新颖的水声信道状态信息（CSI）预测模型，称为CsiPreNet。该模型将一维卷积神经网络（CNN）和长短期记忆（LSTM）网络相结合，以捕捉水声信道在时域和频域的复杂关联性。相比于传统的预测模型，CsiPreNet能够更准确地预测CSI，从而提高自适应水声通信系统的性能。
2. 在线CSI预测模型：论文提出了一种在线CSI预测模型，能够实时地对水声信道的状态进行估计和预测。通过将历史CSI数据与训练的CsiPreNet模型相结合，能够在实时通信过程中快速地预测当前的CSI信息，从而改善传输效率和系统性能。
3. 基于联合子载波-比特-功率分配的资源分配方案：论文还提出了一种基于联合子载波-比特-功率分配的资源分配方案，用于自适应水声OFDMA系统。该方案考虑了计算复杂性、功耗和系统性能等因素，可以根据通信环境和需求，灵活地分配子载波、分配比特和调整功率，以优化系统性能。
4. 离线-在线预测方案：为了应对水声信道的时变特性，论文提出了一种离线-在线预测方案。离线部分主要包括对历史CSI数据的训练和更新，而在线部分则通过训练得到的模型进行实时的CSI估计和预测。该方案能够有效地应对水声信道的动态变化，提高通信系统的稳定性和性能。